Large-scale optimization
Our mission is to develop large-scale optimization techniques and use them to improve the efficiency and robustness of infrastructure at Google.
About the team
We apply techniques from large-scale combinatorial optimization, online algorithms, and control theory to make Google’s computing infrastructure do more with less. We combine online and offline optimizations to achieve goals such as reducing search query latency, increasing model inference throughput and prediction quality, minimizing resource contention, maximizing the efficacy of caches, and eliminating unnecessary work in distributed systems. Our research is used in critical infrastructure that supports Search, Ads, Gemini, YouTube, and Cloud products.
Team focus summaries
Featured publications
Highlighted work
-
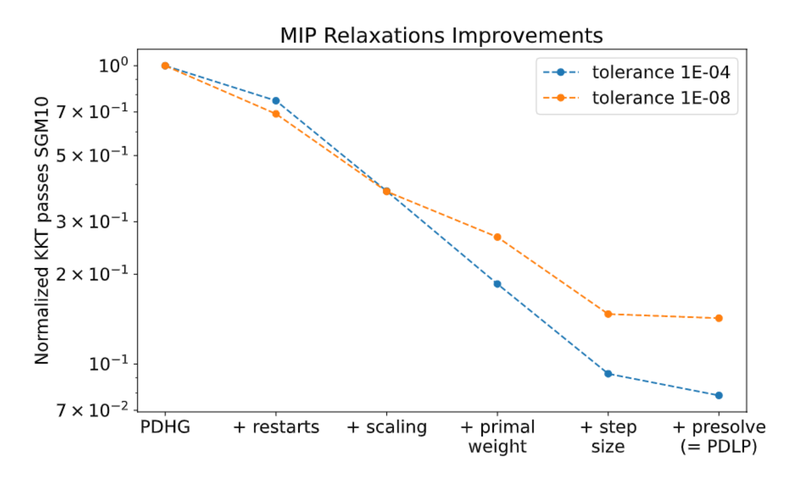 Practical Large-Scale Linear Programming using Primal-Dual Hybrid GradientMathematical background for developers and advanced users of PDLP, a linear and quadratic programming solver available in OR-Tools.
Practical Large-Scale Linear Programming using Primal-Dual Hybrid GradientMathematical background for developers and advanced users of PDLP, a linear and quadratic programming solver available in OR-Tools. -
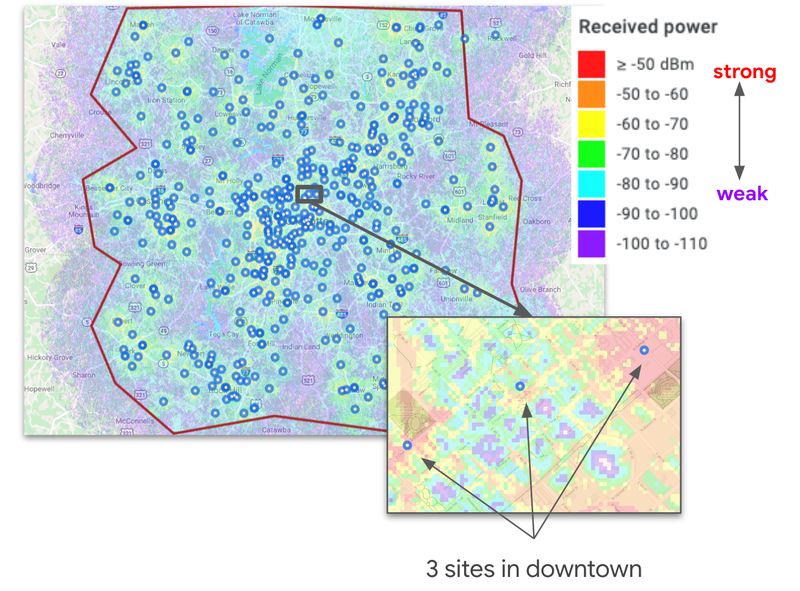 Challenges in Multi-objective Optimization for Automatic Wireless Network PlanningThis blog post describes our efforts to address the most vexing challenges facing telecom network operators, including how we built a scalable auto-planner for wireless telecommunication networks using combinatorial optimization in concert with geospatial and radio propagation modeling.
Challenges in Multi-objective Optimization for Automatic Wireless Network PlanningThis blog post describes our efforts to address the most vexing challenges facing telecom network operators, including how we built a scalable auto-planner for wireless telecommunication networks using combinatorial optimization in concert with geospatial and radio propagation modeling. -
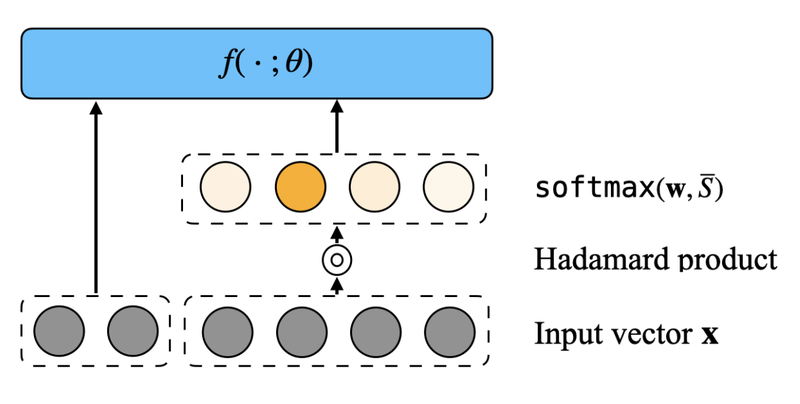 Sequential AttentionWe propose a feature selection algorithm called Sequential Attention (ICLR 2023) that achieves state-of-the-art empirical results for neural networks. This algorithm is an efficient one-pass implementation of greedy forward selection and uses attention weights at each step as a proxy for feature importance.
Sequential AttentionWe propose a feature selection algorithm called Sequential Attention (ICLR 2023) that achieves state-of-the-art empirical results for neural networks. This algorithm is an efficient one-pass implementation of greedy forward selection and uses attention weights at each step as a proxy for feature importance. -
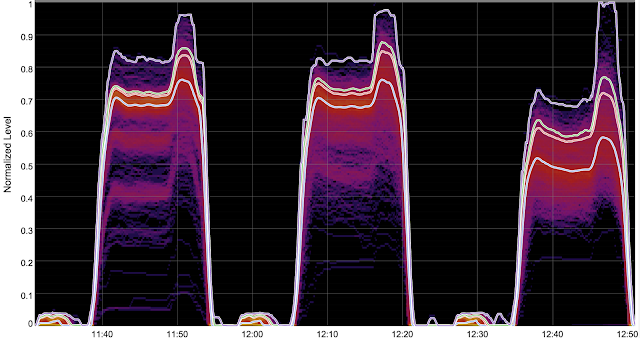 Cache-Aware Load Balancing of Data Center ApplicationsThis paper proposes a method of affinitizing multi-key lookups to minimize cache misses in replicated key-value stores. The method uses offline graph clustering to create a lookup table, paired with a voting scheme to select replicas at serving time. Google web search applied this technique to postings list retrieval, where the improved caching efficiency increased throughput by nearly 50%.
Cache-Aware Load Balancing of Data Center ApplicationsThis paper proposes a method of affinitizing multi-key lookups to minimize cache misses in replicated key-value stores. The method uses offline graph clustering to create a lookup table, paired with a voting scheme to select replicas at serving time. Google web search applied this technique to postings list retrieval, where the improved caching efficiency increased throughput by nearly 50%. -
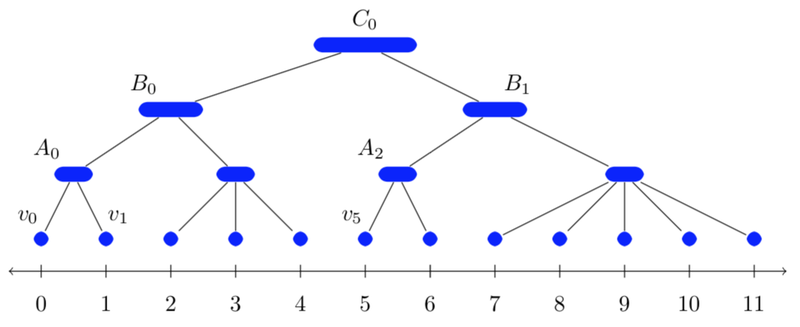 Balanced Partitioning and Hierarchical Clustering at ScaleThis blog post covers our efforts on balanced partitioning and hierarchical clustering at scale. Specifically, it discusses solving large-scale optimization problems and introduces an algorithm for partitioning graphs into clusters to be processed on different machines.
Balanced Partitioning and Hierarchical Clustering at ScaleThis blog post covers our efforts on balanced partitioning and hierarchical clustering at scale. Specifically, it discusses solving large-scale optimization problems and introduces an algorithm for partitioning graphs into clusters to be processed on different machines. -
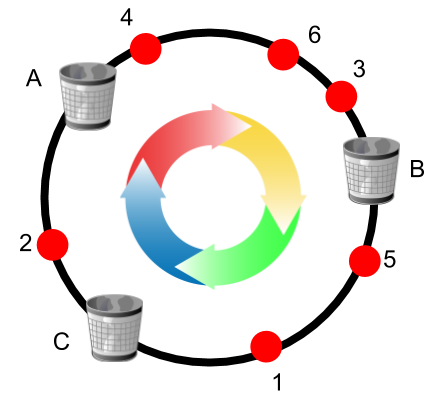 Consistent Hashing with Bounded LoadsThis blog post is about consistent hashing with bounded loads. It discusses balancing loads across servers while allowing servers and clients to be added or removed. We also limit the change to the solution in this dynamic environment. We proposed a novel algorithm that achieves both uniformity and consistency (SODA 2018). Applications of this work have also been discussed in a popular Vimeo engineering blog post.
Consistent Hashing with Bounded LoadsThis blog post is about consistent hashing with bounded loads. It discusses balancing loads across servers while allowing servers and clients to be added or removed. We also limit the change to the solution in this dynamic environment. We proposed a novel algorithm that achieves both uniformity and consistency (SODA 2018). Applications of this work have also been discussed in a popular Vimeo engineering blog post. -
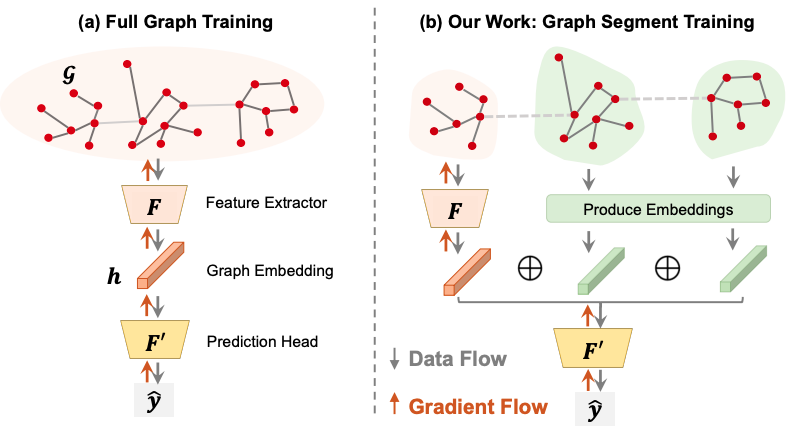 Advancements in Machine Learning for Machine LearningThis blog post presents exciting advancements in ML for ML. In particular, how we use ML to improve efficiency of ML workloads.
Advancements in Machine Learning for Machine LearningThis blog post presents exciting advancements in ML for ML. In particular, how we use ML to improve efficiency of ML workloads. -
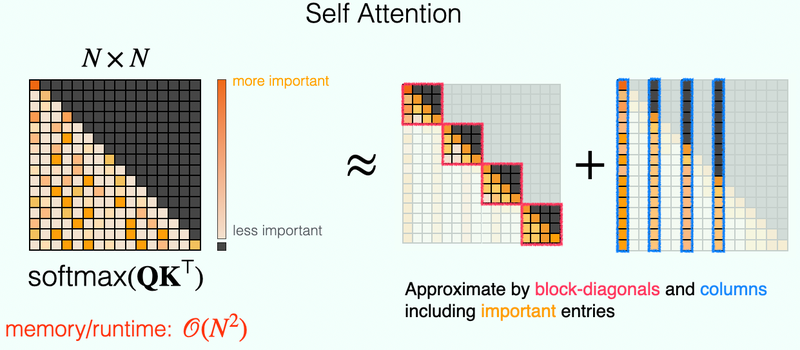 HyperAttention: Large-Scale Attention in Linear TimeThis work introduces a novel approximate self-attention mechanism dubbed "HyperAttention", offering provable linear time complexity in the size of the context while only incurring a negligible loss in downstream quality.
HyperAttention: Large-Scale Attention in Linear TimeThis work introduces a novel approximate self-attention mechanism dubbed "HyperAttention", offering provable linear time complexity in the size of the context while only incurring a negligible loss in downstream quality. -
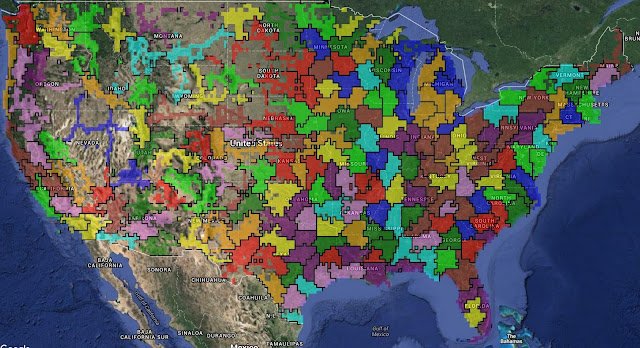 Randomized Experimental Design via Geographic ClusteringThis work studies experimental design in the presence of interference where the treatment of one group may affect the outcomes of others. It shows how to define units or clusters of units with limited interference while maintaining experimental power.
Randomized Experimental Design via Geographic ClusteringThis work studies experimental design in the presence of interference where the treatment of one group may affect the outcomes of others. It shows how to define units or clusters of units with limited interference while maintaining experimental power.
Some of our locations
Some of our people
-

David Applegate
- Algorithms and Theory
-

Aaron Archer
- Algorithms and Theory
- Data Mining and Modeling
- Distributed Systems and Parallel Computing
-

Kevin Aydin
- Algorithms and Theory
- Data Mining and Modeling
- Distributed Systems and Parallel Computing
-

Mohammadhossein Bateni
- Algorithms and Theory
- Data Mining and Modeling
- Distributed Systems and Parallel Computing
-

Lin Chen
- Algorithms and Theory
- Machine Intelligence
-

David Eisenstat
- Algorithms and Theory
-

Matthew Fahrbach
- Algorithms and Theory
- Data Mining and Modeling
- Distributed Systems and Parallel Computing
-

Gang (Thomas) Fu
- Machine Learning
-

Joey Huchette
- Algorithms and Theory
- Machine Intelligence
-

Siddhartha Visveswara Jayanti
- Algorithms and Theory
- Data Mining and Modeling
- Distributed Systems and Parallel Computing
-

Rajesh Jayaram
- Algorithms and Theory
- Data Mining and Modeling
- Distributed Systems and Parallel Computing
-

Vahab S. Mirrokni
- Data Mining and Modeling
- Distributed Systems and Parallel Computing
- Algorithms and Theory
-

Jon Orwant
- Algorithms and Theory
- Distributed Systems and Parallel Computing
- Information Retrieval and the Web
-

Jon Schneider
- Algorithms and Theory
- Economics and Electronic Commerce
-

Morteza Zadimoghaddam
- Algorithms and Theory
- Distributed Systems and Parallel Computing
- Economics and Electronic Commerce
-

Pratik Worah
- Algorithms and Theory
- Machine Intelligence




