Scaling hierarchical agglomerative clustering to trillion-edge graphs
May 1, 2024
Laxman Dhulipala and Jakub Łącki, Research Scientists, Google Research, Graph Mining Team
Quick links
In large-scale prediction and information retrieval tasks, we frequently encounter various applications of clustering, a type of unsupervised machine learning that aims to group similar items together. Examples include de-duplication, anomaly detection, privacy, entity matching, compression, and many more (see more examples in our posts on balanced partitioning and hierarchical clustering at scale, scalability and quality in text clustering, and practical differentially private clustering).
A major challenge is clustering extremely large datasets containing hundreds of billions of datapoints. While multiple high-quality clustering algorithms exist, many of them are not easy to run at scale, often due to their high computational costs or not being designed for parallel multicore or distributed environments. The Graph Mining team within Google Research has been working for many years to develop highly scalable clustering algorithms that deliver high quality.
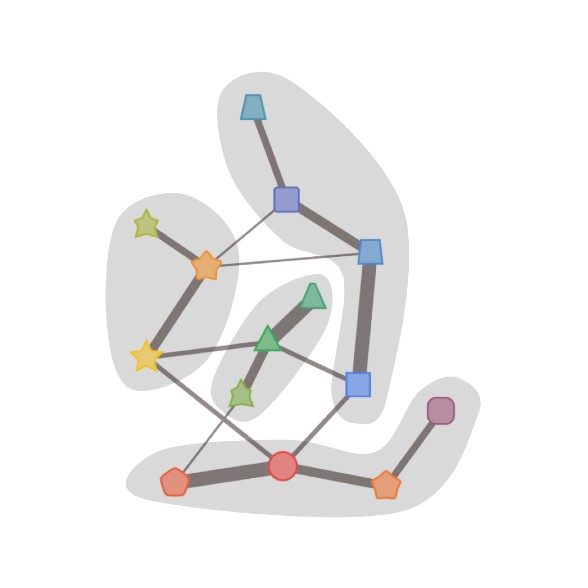
Ten years ago, our colleagues developed a scalable, high-quality algorithm, called affinity clustering, using the simple idea that each datapoint should be in the same cluster as the datapoint it’s most similar to. One can imagine this process as drawing an edge from each point to its nearest neighbor and contracting the connected components. This simple approach was amenable to a scalable MapReduce implementation. However, the guiding principle for the algorithm was not always correct as similarity is not a transitive relation, and the algorithm can erroneously merge clusters due to chaining, i.e., merging long paths of pairwise related concepts to place two unrelated concepts in the same cluster, as illustrated below.
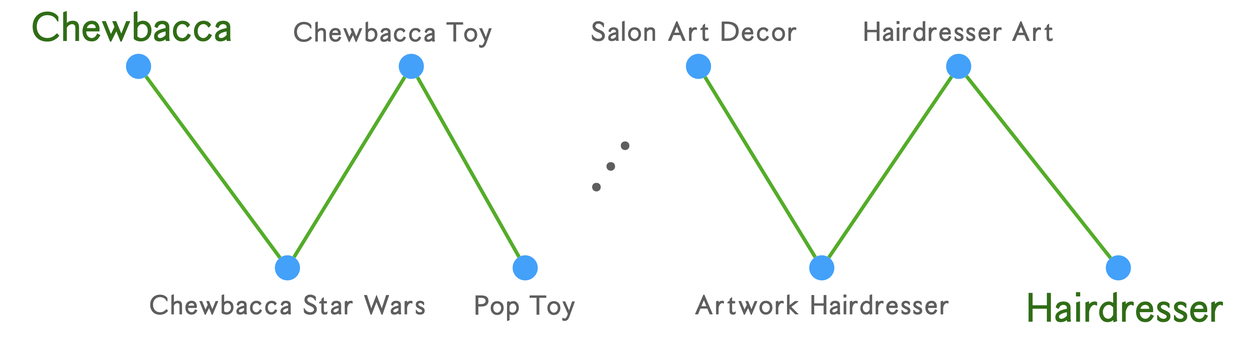
An illustration of chaining in algorithms like affinity clustering.
A big improvement to affinity clustering came with the development of the Sub-Cluster Component (SCC) algorithm, which places a point in the same cluster as its most similar neighbor, only if their similarity is at least a given threshold. Put another way, the algorithm merges connected components induced by edges with similarity that is at least the threshold. Then, the algorithm repeats this approach, and gradually decreases the threshold at each step. Inspired by this line of work on affinity clustering and SCC, we decided to take a fresh look at designing high-quality extremely large-scale clustering algorithms.
In this blogpost, we describe a series of our recent works on building more scalable graph clustering, culminating in our SIGMOD 2024 paper on “TeraHAC: Hierarchical Agglomerative Clustering of Trillion-Edge Graphs”. We cover some of the key ideas behind this work and explain how to scale a high-quality clustering algorithm that can cluster trillion-edge graphs.
Hierarchical agglomerative clustering (HAC)
Both affinity clustering and SCC are inspired by the popular hierarchical agglomerative clustering (HAC) algorithm, a greedy clustering algorithm that is well known to deliver very good clustering quality. The HAC algorithm greedily merges the two closest clusters into a new cluster, proceeding until the desired level of dissimilarity between all pairs of remaining clusters is achieved. HAC can be configured using a linkage function that computes the similarity between two clusters; for example, the popular average-linkage measure computes the similarity of (A, B) as the average similarity between the two sets of points. Average-linkage is a good choice of linkage function as it takes into account the sizes of the clusters that are being merged. However, because HAC performs merges greedily, there is no obvious way to parallelize the algorithm. Moreover, the best previous implementations had quadratic complexity, that is the number of operations they performed was proportional to n², where n is the number of input data points. As a result, HAC could only be applied to moderately sized datasets.

Pseudocode for the HAC algorithm.
Speeding up HAC
In a line of work starting in 2021, we carefully investigated the complexity and parallel scalability of HAC, from a sparse graph-theoretic perspective. We observed that in practice, only m << n² of the most similar entries in the similarity matrix were actually relevant for computing high-quality clusters. Focusing on this sparse setting, we set out to determine if we could design HAC algorithms that exploit sparsity to achieve two key goals:
- a number of computation steps proportional to the number of similarities (m), rather than n², and
- high parallelism and scalability.
We started by carefully exploring the first goal, since achieving this would mean that HAC could be solved much faster on sparse graphs, thus presenting a path for scaling to extremely large datasets. We proved this possibility by presenting an efficient sub-quadratic work algorithm for the problem on sparse graphs which runs in sub-quadratic work (specifically, O(nm½) work, up to poly-logarithmic factors). We obtained the algorithm by designing a careful accounting scheme that combines the classic nearest-neighbor chain algorithm for HAC with a dynamic edge-orientation algorithm.
However, the sub-quadratic work algorithm requires maintaining a complicated dynamic edge-orientation data structure and is not easy to implement. We complemented our exact algorithm with a simple algorithm for approximate average-linkage HAC, which runs in nearly-linear work, i.e., O(m + n) up to poly-logarithmic factors, and is a natural relaxation of the greedy algorithm. Let ε be an accuracy parameter. Then, more formally, a (1+ε)-approximation of HAC is a sequence of cluster merges, where the similarity of each merge is within a factor of (1+ε) of the highest similarity edge in the graph at that time (i.e., the merge that the greedy exact algorithm will perform).
Experimentally, this notion of approximation (say for ε=0.1) incurs a minimal quality loss over the exact algorithm on the same graph. Furthermore, the approximate algorithm also yielded large speedups of over 75× over the quadratic-work algorithms, and could scale to inputs with tens of millions of points. However, our implementations were slow for inputs with more than a few hundred million edges as they were entirely sequential.
The next step was to attempt to design a parallel algorithm that had the same work and a provably low number of sequential dependencies (formally, low depth, i.e., longest critical path). In a pair of papers from NeurIPS 2022 and ICALP 2024, we studied how to obtain good parallel algorithms for HAC. First, we confirmed the common wisdom that exact average-linkage HAC is hard to parallelize due to the sequential dependencies between successive greedy merges. Formally, we showed that the problem is as hard to parallelize as any other problem solvable in polynomial time. Thus, barring a breakthrough in complexity theory, average-linkage HAC is unlikely to admit fast parallel algorithms.
On the algorithmic side, we developed a parallel approximate HAC algorithm, called ParHAC, that we show is highly scalable and runs in near-linear work and poly-logarithmic depth. ParHAC works by grouping the edges into O(log n) weight classes, and processing each class using a carefully designed low-depth symmetry-breaking algorithm. ParHAC enabled the clustering of the WebDataCommons hyperlink graph, one of the largest publicly available graph datasets with over 100 billion edges, in just a few hours using an inexpensive multicore machine.
Sequential HAC (on the left) merges one pair of clusters per step. The parallel algorithm (on the right) can merge multiple pairs of clusters at each step, which results in fewer steps overall.
The TeraHAC algorithm
The final frontier is to obtain scalable and high-quality HAC algorithms when a graph is so large that it no longer fits within the memory of a single machine. In our most recent paper, we designed a new algorithm, called TeraHAC, that scales approximate HAC to trillion-edge graphs. TeraHAC is based on a new approach to computing approximate HAC that is a natural fit for MapReduce-style algorithms. The algorithm proceeds in rounds. In each round, it partitions the graph into subgraphs and then runs on each subgraph independently to make merges. The tricky question is what merges is the algorithm allowed to make?
The main idea behind TeraHAC is to identify a way to perform merges based solely on information local to the subgraphs, while guaranteeing that the merges can be reordered into an approximate merge sequence. The paradox rests in the fact that a cluster in some subgraph may make a merge that is far from being approximate. However, the merges satisfy a certain condition, which allows us to show that the final result of the algorithm is still the same as what a proper (1+ε)-approximate HAC algorithm would have computed.
TeraHAC uses at most a few dozen rounds on all of the graphs used for evaluation, including the largest inputs; our round-complexity is over 100× lower than the best previous approaches to distributed HAC. Our implementation of TeraHAC can compute a high-quality approximate HAC solution on a graph with several trillion edges in under a day using a modest amount of cluster resources (800 hyper-threads over 100 machines). The quality results on this extremely large dataset are shown in the figure below; we see that TeraHAC achieves the best precision-recall tradeoff compared to other scalable clustering algorithms, and is likely the algorithm of choice for very large-scale graph clustering.
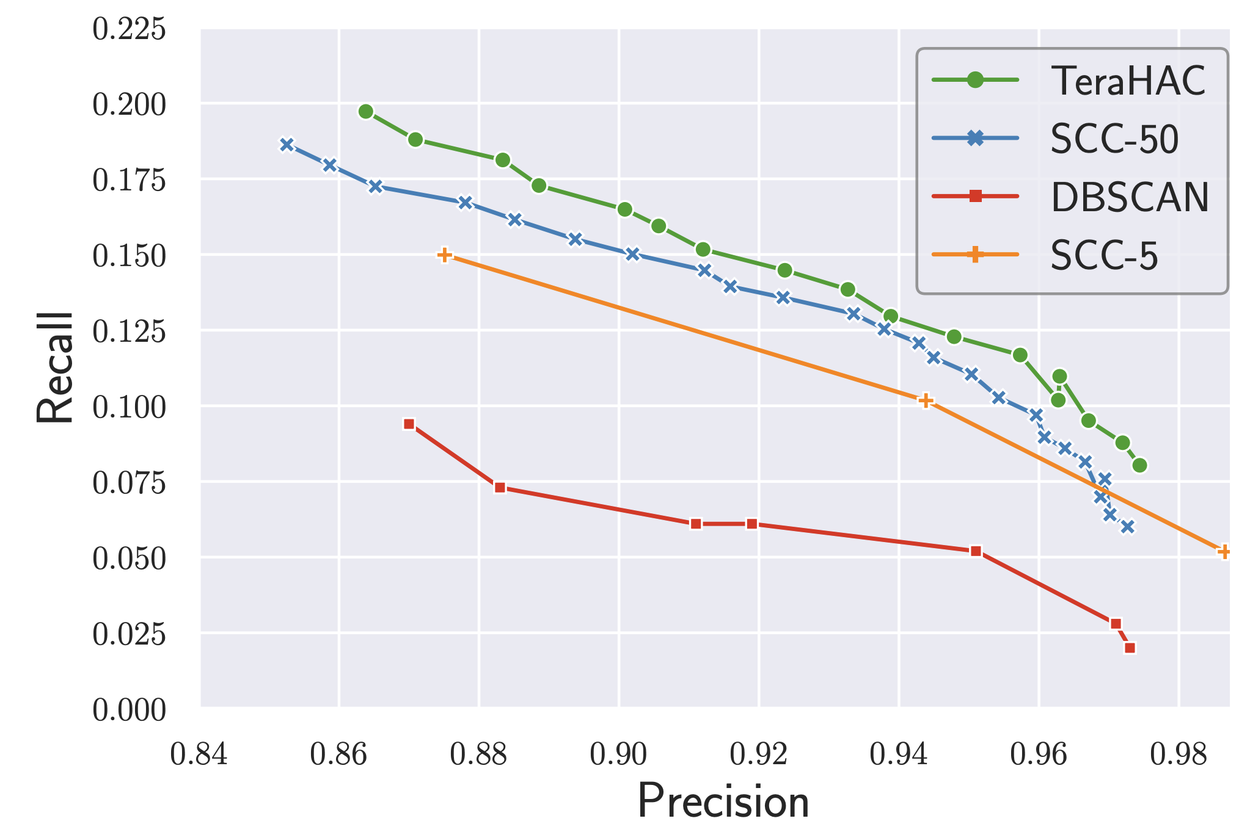
Plot of the precision-recall tradeoff for different large-scale clustering algorithms on an 8-trillion edge dataset.
Conclusion
We demonstrate that despite being a classic method, HAC still has many more secrets to reveal. Interesting directions for future work include designing good dynamic algorithms for HAC (some recent work by our colleagues show promising results in this direction) and understanding the complexity of HAC in low-dimensional metric spaces. Aside from theory, we are hopeful that our team’s approach to scalable and sparse algorithms for hierarchical clustering finds wider use in practice.
Acknowledgements
This blog post reports joint work with our colleagues including MohammadHossein Bateni, David Eisenstat, Rajesh Jayaram, Jason Lee, Vahab Mirrokni and a former intern, Jessica Shi. We also thank our academic collaborators Kishen N Gowda and D Ellis Hershkowitz. Lastly, we thank Tom Small for his valuable help with making the animation in this blog post.


