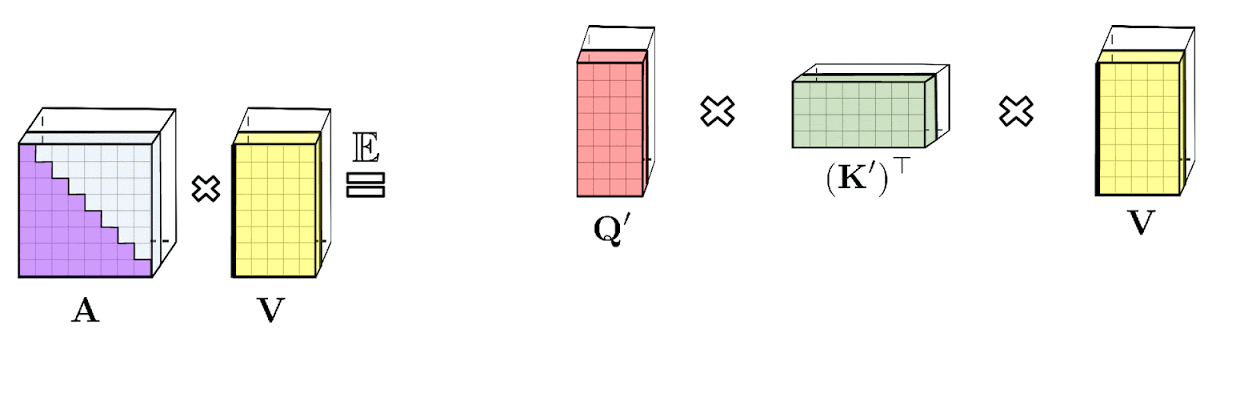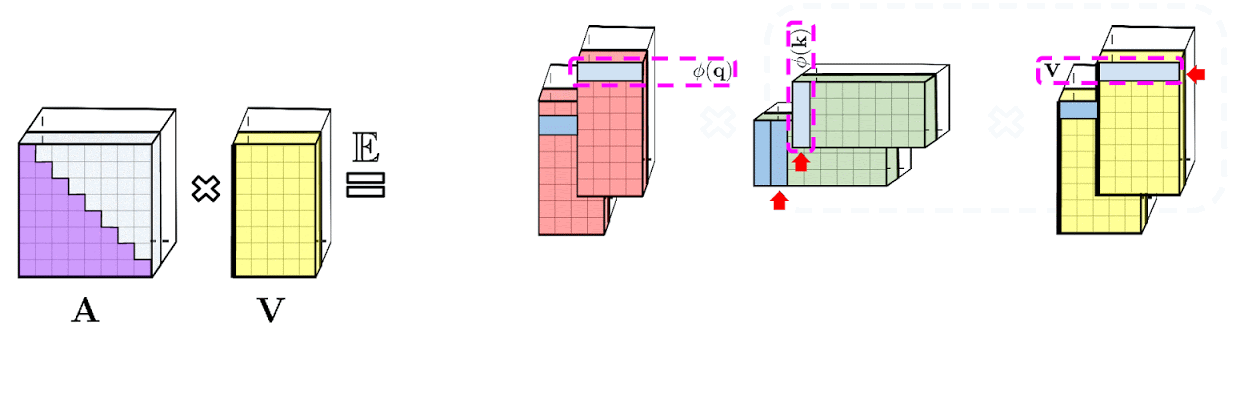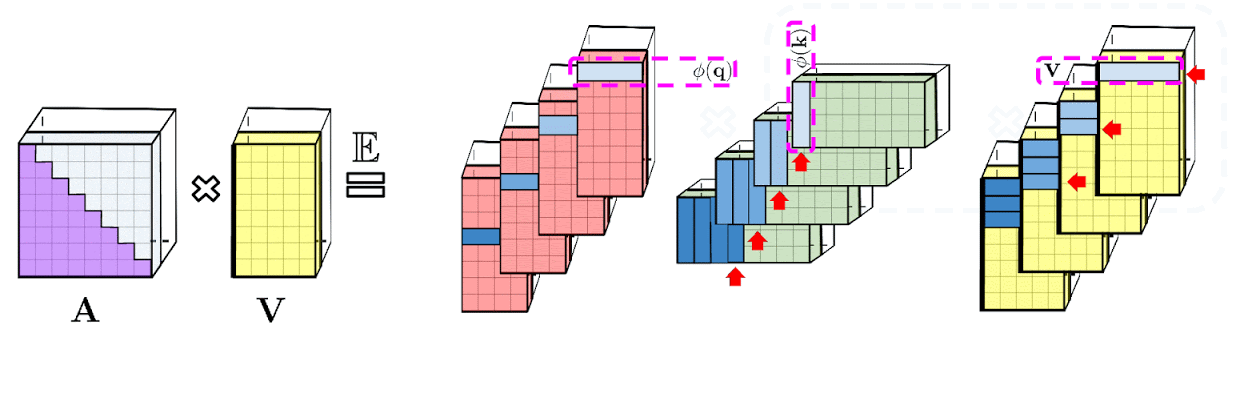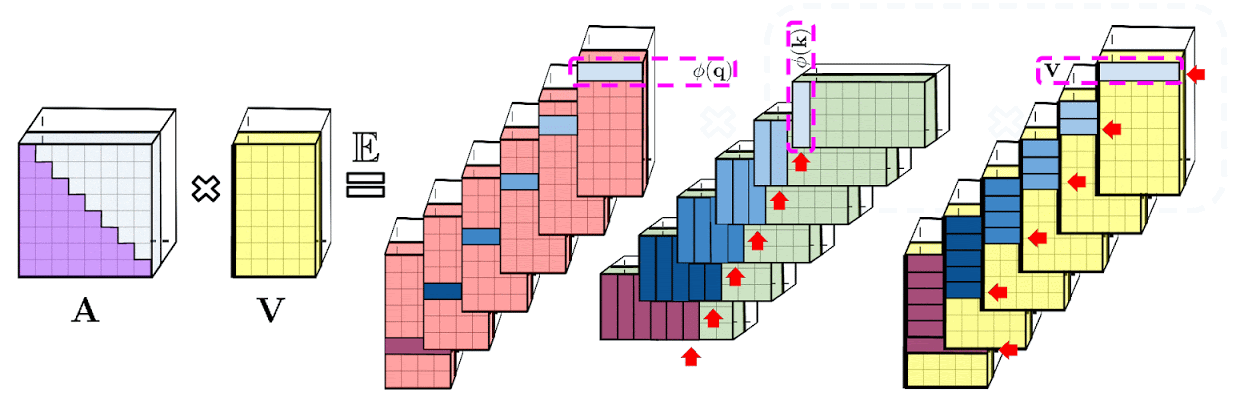Rethinking Attention with Performers

Transformer models have achieved state-of-the-art results across a diverse range of domains, including natural language, conversation, images, and even music. The core block of every Transformer architecture is the attention module, which computes similarity scores for all pairs of positions in an input sequence. This however, scales poorly with the length of the input sequence, requiring quadratic computation time to produce all similarity scores, as well as quadratic memory size to construct a matrix to store these scores.

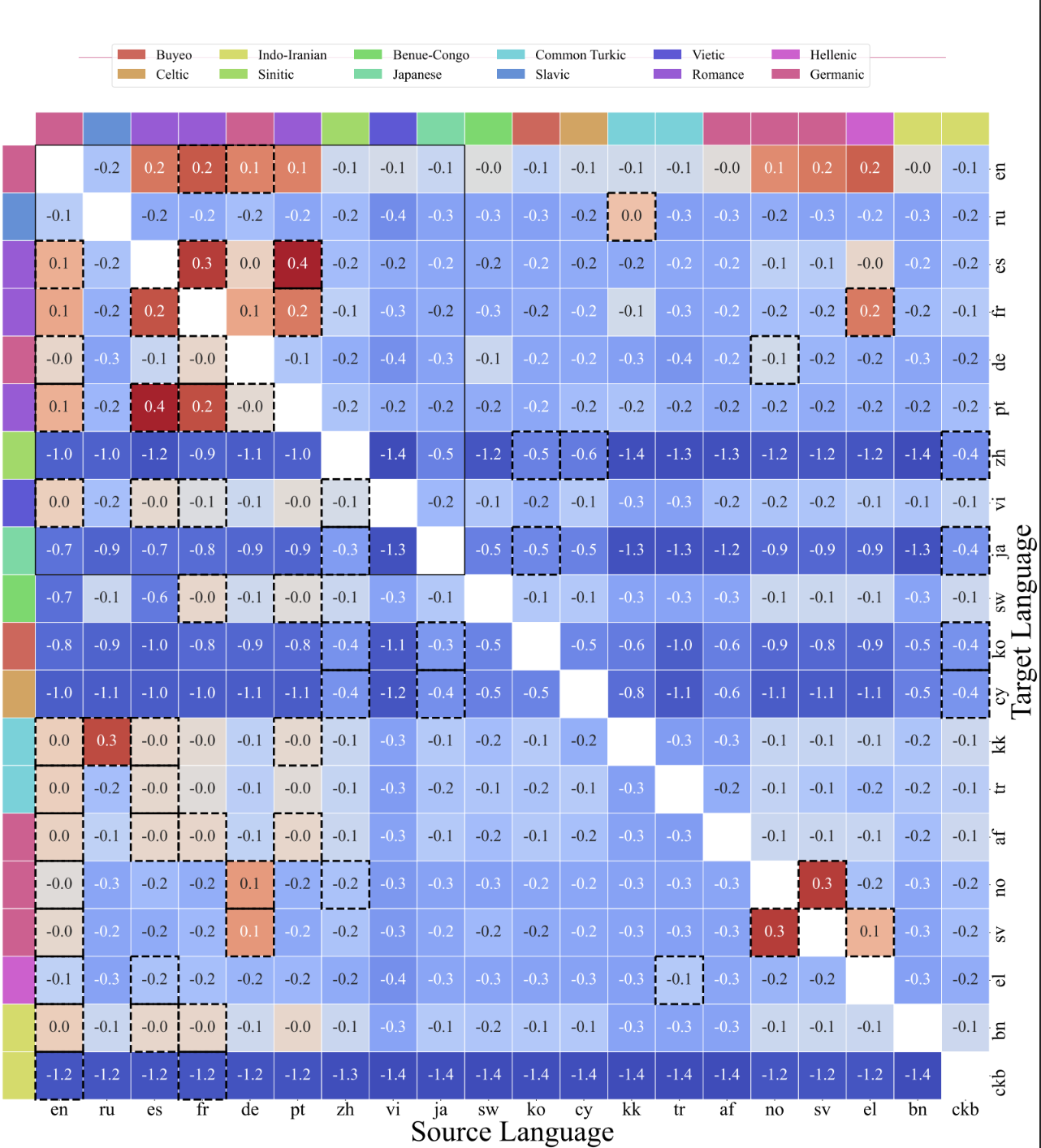
For applications where long-range attention is needed, several fast and more space-efficient proxies have been proposed such as memory caching techniques, but a far more common way is to rely on sparse attention. Sparse attention reduces computation time and the memory requirements of the attention mechanism by computing a limited selection of similarity scores from a sequence rather than all possible pairs, resulting in a sparse matrix rather than a full matrix. These sparse entries may be manually proposed, found via optimization methods, learned, or even randomized, as demonstrated by such methods as Sparse Transformers, Longformers, Routing Transformers, Reformers, and Big Bird. Since sparse matrices can also be represented by graphs and edges, sparsification methods are also motivated by the graph neural network literature, with specific relationships to attention outlined in Graph Attention Networks. Such sparsity-based architectures usually require additional layers to implicitly produce a full attention mechanism.

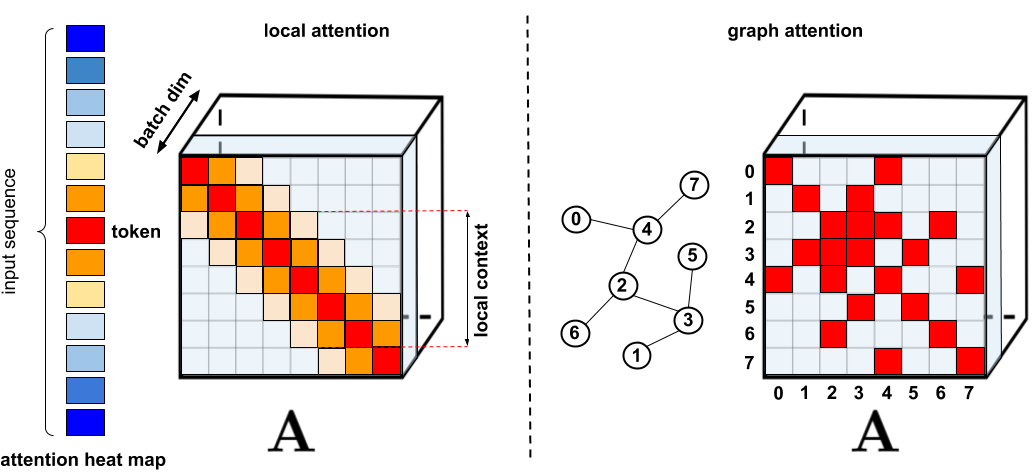Standard sparsification techniques. Left: Example of a sparsity pattern, where tokens attend only to other nearby tokens. Right: In Graph Attention Networks, tokens attend only to their neighbors in the graph, which should have higher relevance than other nodes. See Efficient Transformers: A Survey for a comprehensive categorization of various methods.

Unfortunately, sparse attention methods can still suffer from a number of limitations. (1) They require efficient sparse-matrix multiplication operations, which are not available on all accelerators; (2) they usually do not provide rigorous theoretical guarantees for their representation power; (3) they are optimized primarily for Transformer models and generative pre-training; and (4) they usually stack more attention layers to compensate for sparse representations, making them difficult to use with other pre-trained models, thus requiring retraining and significant energy consumption. In addition to these shortcomings, sparse attention mechanisms are often still not sufficient to address the full range of problems to which regular attention methods are applied, such as Pointer Networks. There are also some operations that cannot be sparsified, such as the commonly used softmax operation, which normalizes similarity scores in the attention mechanism and is used heavily in industry-scale recommender systems.

To resolve these issues, we introduce the Performer, a Transformer architecture with attention mechanisms that scale linearly, thus enabling faster training while allowing the model to process longer lengths, as required for certain image datasets such as ImageNet64 and text datasets such as PG-19. The Performer uses an efficient (linear) generalized attention framework, which allows a broad class of attention mechanisms based on different similarity measures (kernels). The framework is implemented by our novel Fast Attention Via Positive Orthogonal Random Features (FAVOR+) algorithm, which provides scalable low-variance and unbiased estimation of attention mechanisms that can be expressed by random feature map decompositions (in particular, regular softmax-attention). We obtain strong accuracy guarantees for this method while preserving linear space and time complexity, which can also be applied to standalone softmax operations.

Generalized Attention
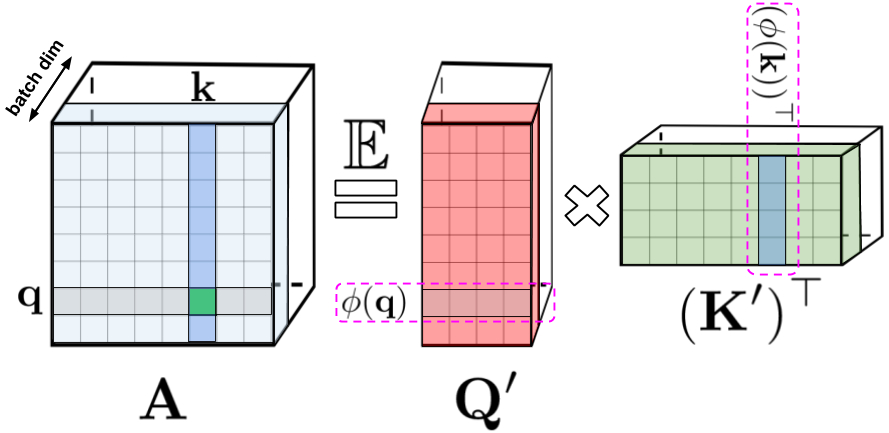
In the original attention mechanism, the query and key inputs, corresponding respectively to rows and columns of a matrix, are multiplied together and passed through a softmax operation to form an attention matrix, which stores the similarity scores. Note that in this method, one cannot decompose the query-key product back into its original query and key components after passing it into the nonlinear softmax operation. However, it is possible to decompose the attention matrix back to a product of random nonlinear functions of the original queries and keys, otherwise known as random features, which allows one to encode the similarity information in a more efficient manner.

LHS: The standard attention matrix, which contains all similarity scores for every pair of entries, formed by a softmax operation on the query and keys, denoted by q and k. RHS: The standard attention matrix can be approximated via lower-rank randomized matrices Q′ and K′ with rows encoding potentially randomized nonlinear functions of the original queries/keys. For the regular softmax-attention, the transformation is very compact and involves an exponential function as well as random Gaussian projections.

Regular softmax-attention can be seen as a special case with these nonlinear functions defined by exponential functions and Gaussian projections. Note that we can also reason inversely, by implementing more general nonlinear functions first, implicitly defining other types of similarity measures, or kernels, on the query-key product. We frame this as generalized attention, based on earlier work in kernel methods. Although for most kernels, closed-form formulae do not exist, our mechanism can still be applied since it does not rely on them.

To the best of our knowledge, we are the first to show that any attention matrix can be effectively approximated in downstream Transformer-applications using random features. The novel mechanism enabling this is the use of positive random features, i.e., positive-valued nonlinear functions of the original queries and keys, which prove to be crucial for avoiding instabilities during training and provide more accurate approximation of the regular softmax attention mechanism.

Towards FAVOR+: Fast Attention via Matrix Associativity
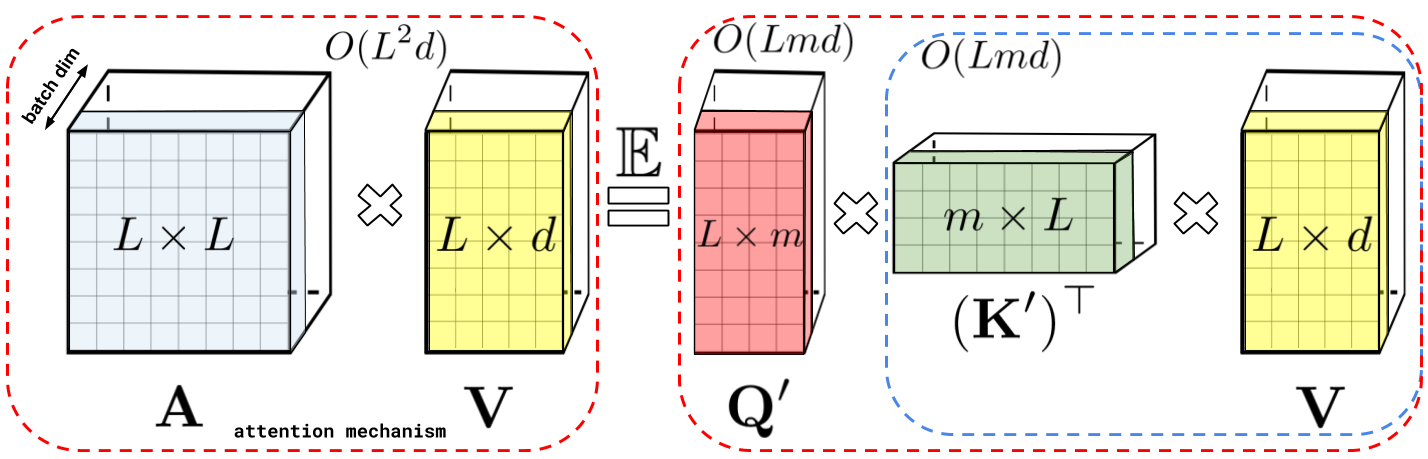
The decomposition described above allows one to store the implicit attention matrix with linear, rather than quadratic, memory complexity. One can also obtain a linear time attention mechanism using this decomposition. While the original attention mechanism multiplies the stored attention matrix with the value input to obtain the final result, after decomposing the attention matrix, one can rearrange matrix multiplications to approximate the result of the regular attention mechanism, without explicitly constructing the quadratic-sized attention matrix. This ultimately leads to FAVOR+.

Left: Standard attention module computation, where the final desired result is computed by performing a matrix multiplication with the attention matrix A and value tensor V. Right: By decoupling matrices Q′ and K′ used in lower rank decomposition of A and conducting matrix multiplications in the order indicated by dashed-boxes, we obtain a linear attention mechanism, never explicitly constructing A or its approximation.

The above analysis is relevant for so-called bidirectional attention, i.e., non-causal attention where there is no notion of past and future. For unidirectional (causal) attention, where tokens do not attend to other tokens appearing later in the input sequence, we slightly modify the approach to use prefix-sum computations, which only store running totals of matrix computations rather than storing an explicit lower-triangular regular attention matrix.

Left: Standard unidirectional attention requires masking the attention matrix to obtain its lower-triangular part. Right: Unbiased approximation on the LHS can be obtained via a prefix-sum mechanism, where the prefix-sum of the outer-products of random feature maps for keys and value vectors is built on the fly and left-multiplied by query random feature vector to obtain the new row in the resulting matrix.

Properties
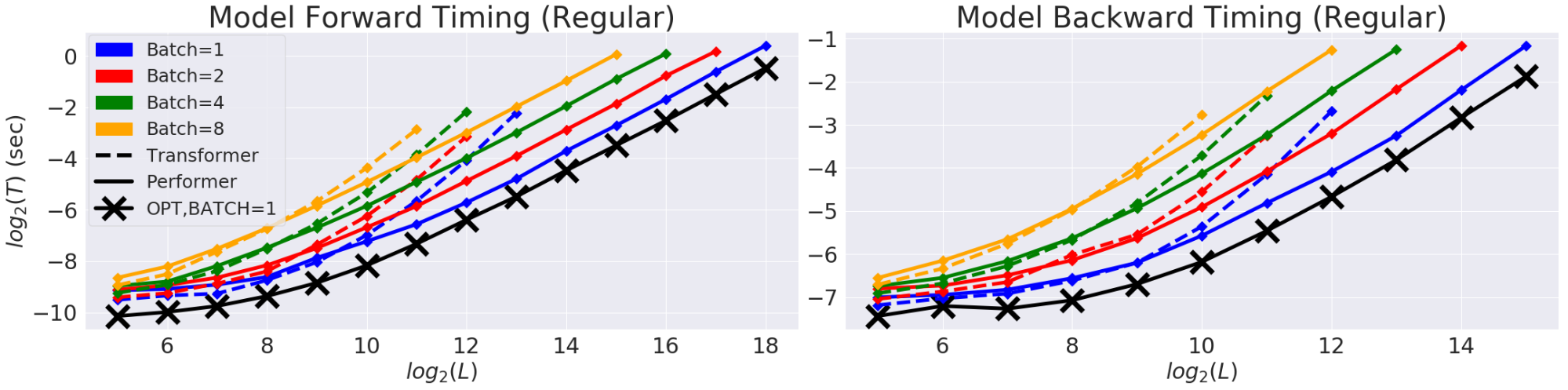
We first benchmark the space- and time-complexity of the Performer and show that the attention speedups and memory reductions are empirically nearly optimal, i.e., very close to simply not using an attention mechanism at all in the model.

Bidirectional timing for the regular Transformer model in log-log plot with time (T) and length (L). Lines end at the limit of GPU memory. The black line (X) denotes the maximum possible memory compression and speedups when using a “dummy” attention block, which essentially bypasses attention calculations and demonstrates the maximum possible efficiency of the model. The Performer model is nearly able to reach this optimal performance in the attention component.

We further show that the Performer, using our unbiased softmax approximation, is backwards compatible with pretrained Transformer models after a bit of fine-tuning, which could potentially lower energy costs by improving inference speed, without having to fully retrain pre-existing models.

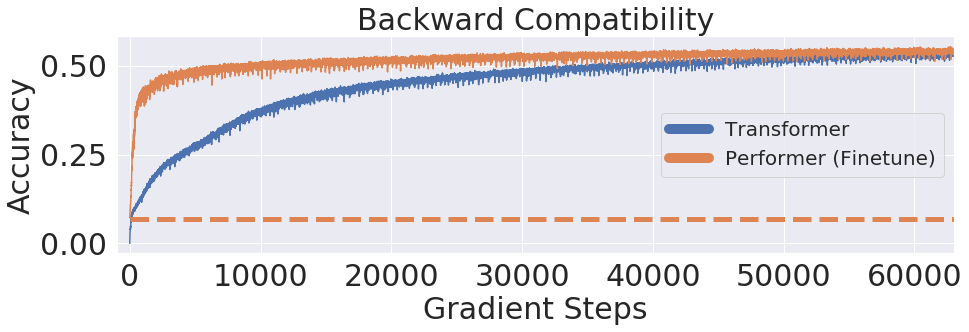Using the One Billion Word Benchmark (LM1B) dataset, we transferred the original pre-trained Transformer weights to the Performer model, which produces an initial non-zero 0.07 accuracy (dotted orange line). Once fine-tuned however, the Performer quickly recovers accuracy in a small fraction of the original number of gradient steps.

Example Application: Protein Modeling
Proteins are large molecules with complex 3D structures and specific functions that are essential to life. Like words, proteins are specified as linear sequences where each character is one of 20 amino acid building blocks. Applying Transformers to large unlabeled corpora of protein sequences (e.g. UniRef) yields models that can be used to make accurate predictions about the folded, functional macromolecule. Performer-ReLU (which uses ReLU-based attention, an instance of generalized attention that is different from softmax) performs strongly at modeling protein sequence data, while Performer-Softmax matches the performance of the Transformer, as predicted by our theoretical results.

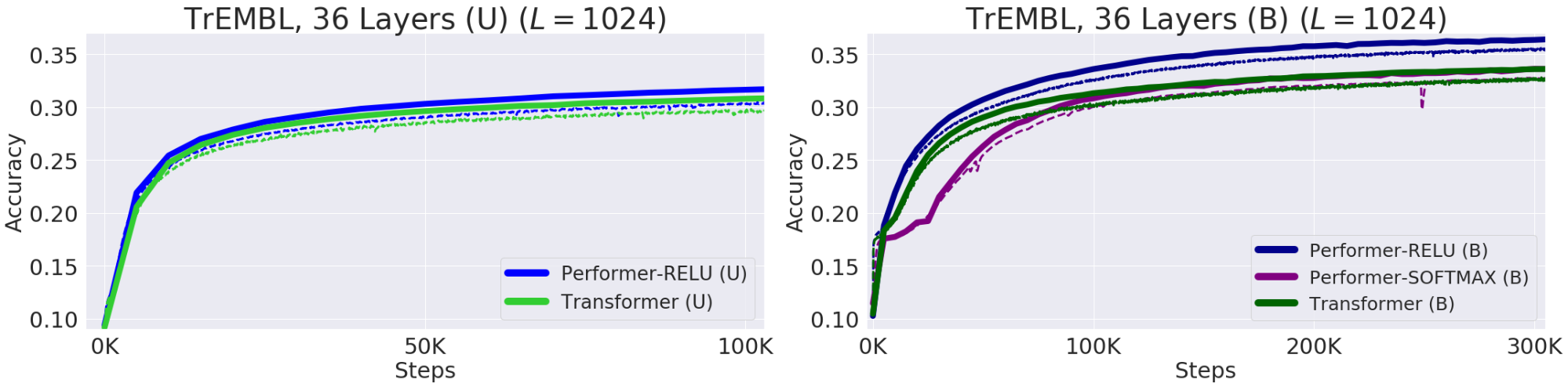Performance at modeling protein sequences. Train = Dashed, Validation = Solid, Unidirectional = (U), Bidirectional = (B). We use the 36-layer model parameters from ProGen (2019) for all runs, each using a 16x16 TPU-v2. Batch sizes were maximized for each run, given the corresponding compute constraints.

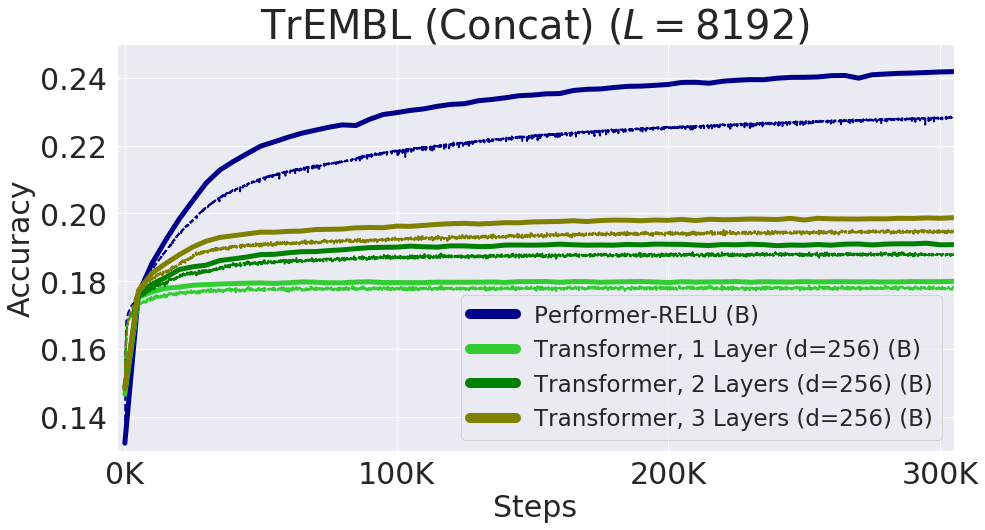
Below we visualize a protein Performer model, trained using the ReLU-based approximate attention mechanism. Using the Performer to estimate similarity between amino acids recovers similar structure to well-known substitution matrices obtained by analyzing evolutionary substitution patterns across carefully curated sequence alignments. More generally, we find local and global attention patterns consistent with Transformer models trained on protein data. The dense attention approximation of the Performer has the potential to capture global interactions across multiple protein sequences. As a proof of concept, we train models on long concatenated protein sequences, which overloads the memory of a regular Transformer model, but not the Performer due to its space efficiency.

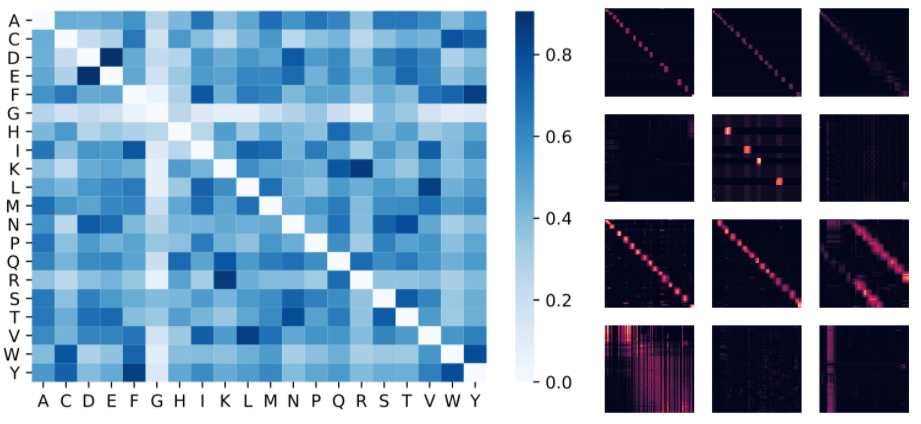Left: Amino acid similarity matrix estimated from attention weights. The model recognizes highly similar amino acid pairs such as (D,E) and (F,Y), despite only having access to protein sequences without prior information about biochemistry. Center: Attention matrices from 4 layers (rows) and 3 selected heads (columns) for the BPT1_BOVIN protein, showing local and global attention patterns.

Performance on sequences up to length 8192 obtained by concatenating individual protein sequences. To fit into TPU memory, the Transformer’s size (number of layers and embedding dimensions) was reduced.

Conclusion
Our work contributes to the recent efforts on non-sparsity based methods and kernel-based interpretations of Transformers. Our method is interoperable with other techniques like reversible layers and we have even integrated FAVOR with the Reformer's code. We provide the links for the paper, Performer code, and the Protein Language Modeling code. We believe that our research opens up a brand new way of thinking about attention, Transformer architectures, and even kernel methods.

Acknowledgements
This work was performed by the core Performer designers Krzysztof Choromanski (Google Brain Team, Tech and Research Lead), Valerii Likhosherstov (University of Cambridge) and Xingyou Song (Google Brain Team), with contributions from David Dohan, Andreea Gane, Tamas Sarlos, Peter Hawkins, Jared Davis, Afroz Mohiuddin, Lukasz Kaiser, David Belanger, Lucy Colwell, and Adrian Weller. We give special thanks to the Applied Science Team for jointly leading the research effort on applying efficient Transformer architectures to protein sequence data.

We additionally wish to thank Joshua Meier, John Platt, and Tom Weingarten for many fruitful discussions on biological data and useful comments on this draft, along with Yi Tay and Mostafa Dehghani for discussions on comparing baselines. We further thank Nikita Kitaev and Wojciech Gajewski for multiple discussions on the Reformer, and Aurko Roy and Ashish Vaswani for multiple discussions on the Routing Transformer.