Introducing Nested Learning: A new ML paradigm for continual learning
November 7, 2025
Ali Behrouz, Student Researcher, and Vahab Mirrokni, VP and Google Fellow, Google Research
We introduce Nested Learning, a new approach to machine learning that views models as a set of smaller, nested optimization problems, each with its own internal workflow, in order to mitigate or even completely avoid the issue of “catastrophic forgetting”, where learning new tasks sacrifices proficiency on old tasks.
Quick links
The last decade has seen incredible progress in machine learning (ML), primarily driven by powerful neural network architectures and the algorithms used to train them. However, despite the success of large language models (LLMs), a few fundamental challenges persist, especially around continual learning, the ability for a model to actively acquire new knowledge and skills over time without forgetting old ones.
When it comes to continual learning and self-improvement, the human brain is the gold standard. It adapts through neuroplasticity — the remarkable capacity to change its structure in response to new experiences, memories, and learning. Without this ability, a person is limited to immediate context (like anterograde amnesia). We see a similar limitation in current LLMs: their knowledge is confined to either the immediate context of their input window or the static information that they learn during pre-training.
The simple approach, continually updating a model's parameters with new data, often leads to “catastrophic forgetting” (CF), where learning new tasks sacrifices proficiency on old tasks. Researchers traditionally combat CF through architectural tweaks or better optimization rules. However, for too long, we have treated the model's architecture (the network structure) and the optimization algorithm (the training rule) as two separate things, which prevents us from achieving a truly unified, efficient learning system.
In our paper, “Nested Learning: The Illusion of Deep Learning Architectures”, published at NeurIPS 2025, we introduce Nested Learning, which bridges this gap. Nested Learning treats a single ML model not as one continuous process, but as a system of interconnected, multi-level learning problems that are optimized simultaneously. We argue that the model's architecture and the rules used to train it (i.e., the optimization algorithm) are fundamentally the same concepts; they are just different "levels" of optimization, each with its own internal flow of information ("context flow") and update rate. By recognizing this inherent structure, Nested Learning provides a new, previously invisible dimension for designing more capable AI, allowing us to build learning components with deeper computational depth, which ultimately helps solve issues like catastrophic forgetting.
We test and validate Nested Learning through a proof-of-concept, self-modifying architecture that we call “Hope”, which achieves superior performance in language modeling and demonstrates better long-context memory management than existing state-of-the-art models.
The Nested Learning paradigm
Nested Learning reveals that a complex ML model is actually a set of coherent, interconnected optimization problems nested within each other or running in parallel. Each of these internal problems has its own context flow — its own distinct set of information from which it is trying to learn.
This perspective implies that existing deep learning methods work by essentially compressing their internal context flows. More importantly, Nested Learning reveals a new dimension for designing models, allowing us to build learning components with deeper computational depth.
To illustrate this paradigm, we look at the concept of associative memory — the ability to map and recall one thing based on another (like recalling a name when you see a face).
- We show that the training process itself, specifically the backpropagation process, can be modeled as an associative memory. The model learns to map a given data point to the value of its local error, which serves as a measure of how "surprising" or unexpected that data point was.
- Similarly, following previous studies (e.g., Miras), key architectural components, such as the attention mechanism in transformers, can also be formalized as simple associative memory modules that learn the mapping between tokens in a sequence.

The uniform and reusable structure as well as multi-time–scale update in the brain are the key components of continual learning in humans. Nested Learning allows for multi-time–scale updates for each component of the brain, while showing that well-known architectures such as transformers and memory modules are in fact linear layers with different frequency updates.
By defining an update frequency rate, i.e., how often each component's weights are adjusted, we can order these interconnected optimization problems into "levels." This ordered set forms the heart of the Nested Learning paradigm.
Putting Nested Learning to work
The Nested Learning perspective immediately gives us principled ways to improve existing algorithms and architectures:
Deep optimizers
Since Nested Learning views optimizers (e.g., momentum-based optimizers) as associative memory modules, it allows us to apply principles from associative memory perspective to them. We observed that many standard optimizers rely on simple dot-product similarity (a measure of how alike two vectors are by calculating the sum of the products of their corresponding components) whose update doesn't account for how different data samples relate to each other. By changing the underlying objective of the optimizer to a more standard loss metric, such as L2 regression loss (a common loss function in regression tasks that quantifies the error by summing the squares of the differences between predicted and true values), we derive new formulations for core concepts like momentum, making them more resilient to imperfect data.
Continuum memory systems
In a standard Transformer, the sequence model acts as a short-term memory, holding the immediate context, while the feedforward neural networks act as long-term memory, storing pre-training knowledge. The Nested Learning paradigm extends this concept into what we call a “continuum memory system” (CMS), where memory is seen as a spectrum of modules, each updating at a different, specific frequency rate. This creates a much richer and more effective memory system for continual learning.
Hope: A self-modifying architecture with continuum memory
As a proof-of-concept, we used Nested Learning principles to design Hope, a variant of the Titans architecture. Titans architectures are long-term memory modules that prioritize memories based on how surprising they are. Despite their powerful memory management, they only have two levels of parameters update, resulting in a first-order in-context learning. Hope, however, is a self-modifying recurrent architecture that can take advantage of unbounded levels of in-context learning and also is augmented with CMS blocks to scale to larger context windows. It can essentially optimize its own memory through a self-referential process, creating an architecture with infinite, looped learning levels.
Experiments
We conducted experiments to evaluate the effectiveness of our deep optimizers and the performance of Hope on language modeling, long-context reasoning, continual learning, and knowledge incorporation tasks. The full results are available in our paper.
Results
Our experiments confirm the power of Nested Learning, the design of continuum memory systems, and self-modifying Titans.
On a diverse set of commonly used and public language modeling and common-sense reasoning tasks, the Hope architecture demonstrates lower perplexity and higher accuracy compared to modern recurrent models and standard transformers.
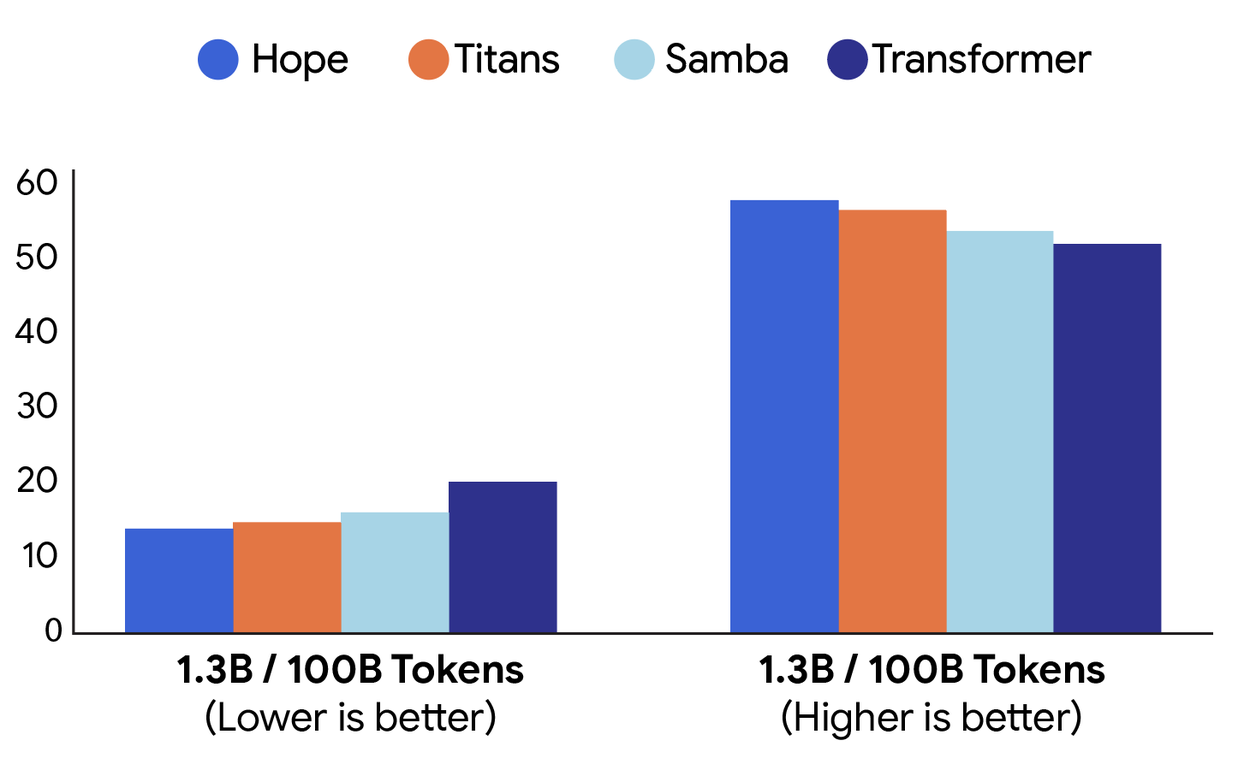
Comparison of performance on language modeling (perplexity; left) and common-sense reasoning (accuracy; right) tasks between different architectures: Hope, Titans, Samba and a baseline Transformer.
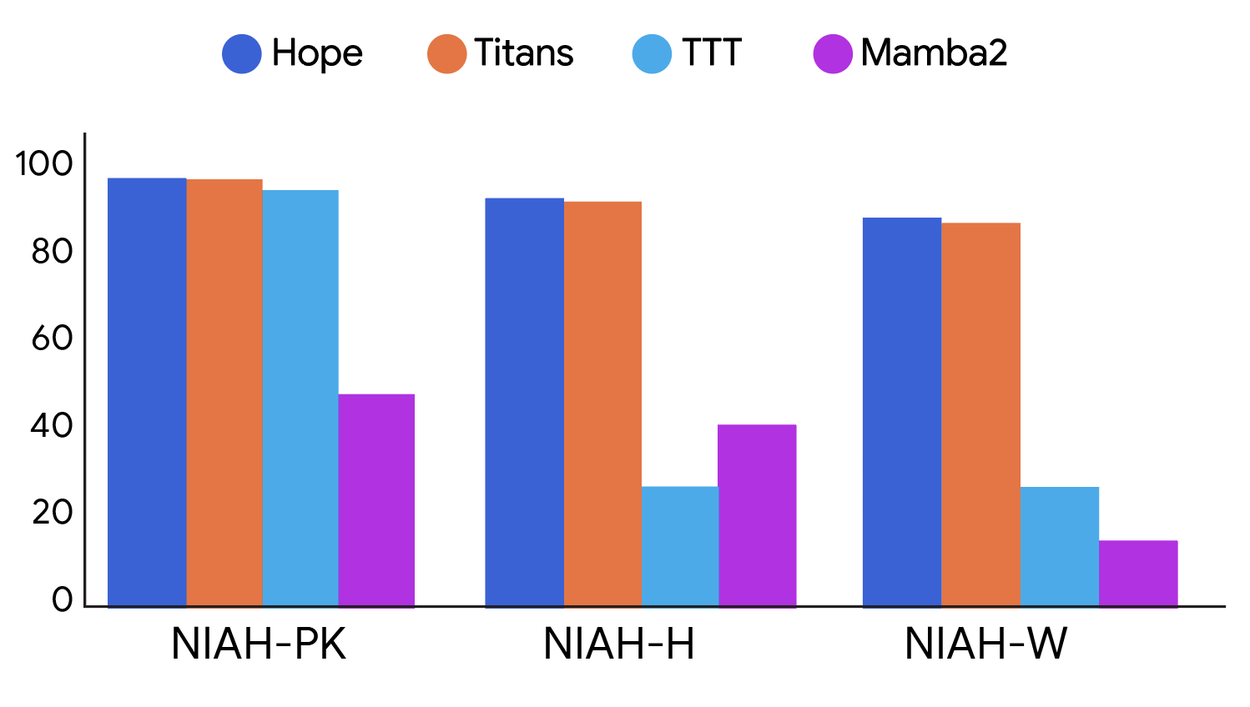
Hope showcases superior memory management in long-context Needle-In-Haystack (NIAH) downstream tasks, proving that the CMSs offer a more efficient and effective way to handle extended sequences of information.
Conclusion
The Nested Learning paradigm represents a step forward in our understanding of deep learning. By treating architecture and optimization as a single, coherent system of nested optimization problems, we unlock a new dimension for design, stacking multiple levels. The resulting models, like the Hope architecture, show that a principled approach to unifying these elements can lead to more expressive, capable, and efficient learning algorithms.
We believe the Nested Learning paradigm offers a robust foundation for closing the gap between the limited, forgetting nature of current LLMs and the remarkable continual learning abilities of the human brain. We are excited for the research community to explore this new dimension and help us build the next generation of self-improving AI.
Acknowledgements
This research was conducted by Ali Behrouz, Meisam Razaviyayn, Peilin Zhong, and Vahab Mirrokni. We thank Praneeth Kacham and Corinna Cortes for reviewing the work and their valuable suggestions. We also thank Yuan Deng and Zeman Li. Finally, we thank Mark Simborg and Kimberly Schwede for their help in crafting this blog post.