Introducing GIST: The next stage in smart sampling
January 23, 2026
Morteza Zadimoghaddam and Matthew Fahrbach, Research Scientists, Google Research
We introduce GIST, a novel algorithm that provides provable guarantees for selecting a high-quality data subset that maximizes both data diversity and data utility.
Quick links
Modern machine learning (ML) has unlocked unprecedented performance at the cost of having to process increasingly massive and complex datasets. From large language models (LLMs) to computer vision systems, there’s a common challenge: handling a massive amount of data that’s expensive to process.
This necessitates subset selection — the task of choosing a smaller, representative group of data points from the full dataset for the typical training task (not the fine-tuning). The question is then: how can we be sure this subset contains enough information to train an accurate model?
At NeurIPS 2025, we introduced Greedy Independent Set Thresholding (GIST), a novel algorithm that helps solve this issue by balancing data “diversity” (ensuring the selected data is not redundant) and data “utility“ (data that is relevant and useful for the task). GIST not only outperforms state-of-the-art benchmarks tasks, such as image classification, but it does so with a mathematical guarantee about its solution quality.
The conflict: Why smart sampling is hard
When selecting a subset of data, researchers must balance two often conflicting objectives: diversity and utility. Enforcing data diversity ensures the selected points aren’t redundant. Utility measures the overall usefulness or informational value of the selected subset.
For diversity, we focus on maximizing the minimum distance (typically in embedding space) between any two selected data points, also known as max-min diversity. If you choose two data points that are very similar (e.g., two almost identical pictures of a golden retriever), your diversity is low. Max-min diversity forces you to select points that are all as far apart from each other as possible, minimizing redundancy and ensuring broad coverage of the data landscape. For utility, we focus on the class of monotone submodular functions, which aim to maximize the total unique information covered by the subset.
The difficulty lies in combining these two goals. A pure max-min strategy might select diverse but ultimately irrelevant data points, while a pure utility strategy might select a tight, highly relevant cluster of redundant points. Finding a subset that is both maximally spread out and maximally informative is a complex combinatorial problem that is known to be NP-hard, meaning that no algorithm can find the best solution efficiently, especially for massive datasets.
This inherent conflict requires a clever approximation strategy.
How GIST works
Since finding a perfect subset is impractical, the goal shifts to finding an algorithm with a provable approximation guarantee — a mathematical safety net that assures the solution is always close to the true optimum. This is where GIST provides its groundbreaking solution.
GIST breaks the diversity–utility challenge into a series of simpler, but related, optimization problems:
1. Thresholding the diversity component
GIST starts by temporarily isolating the diversity component. Instead of trying to maximize the minimum distance between all points (the hard part), GIST tackles a simpler question: "For a certain fixed minimum distance, what is the best subset of data we can select?"
By fixing the minimum required distance, GIST processes the data using a graph where two points are connected only if their distance is less than that specified distance. In this graph, any two connected points are considered too similar to be in the final subset.
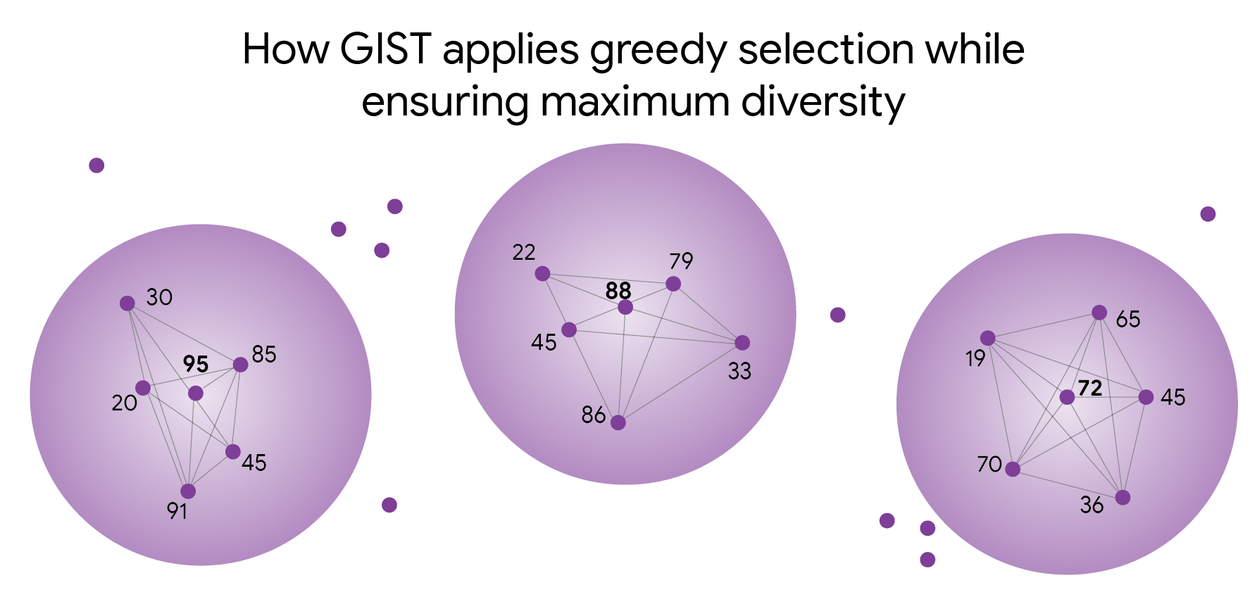
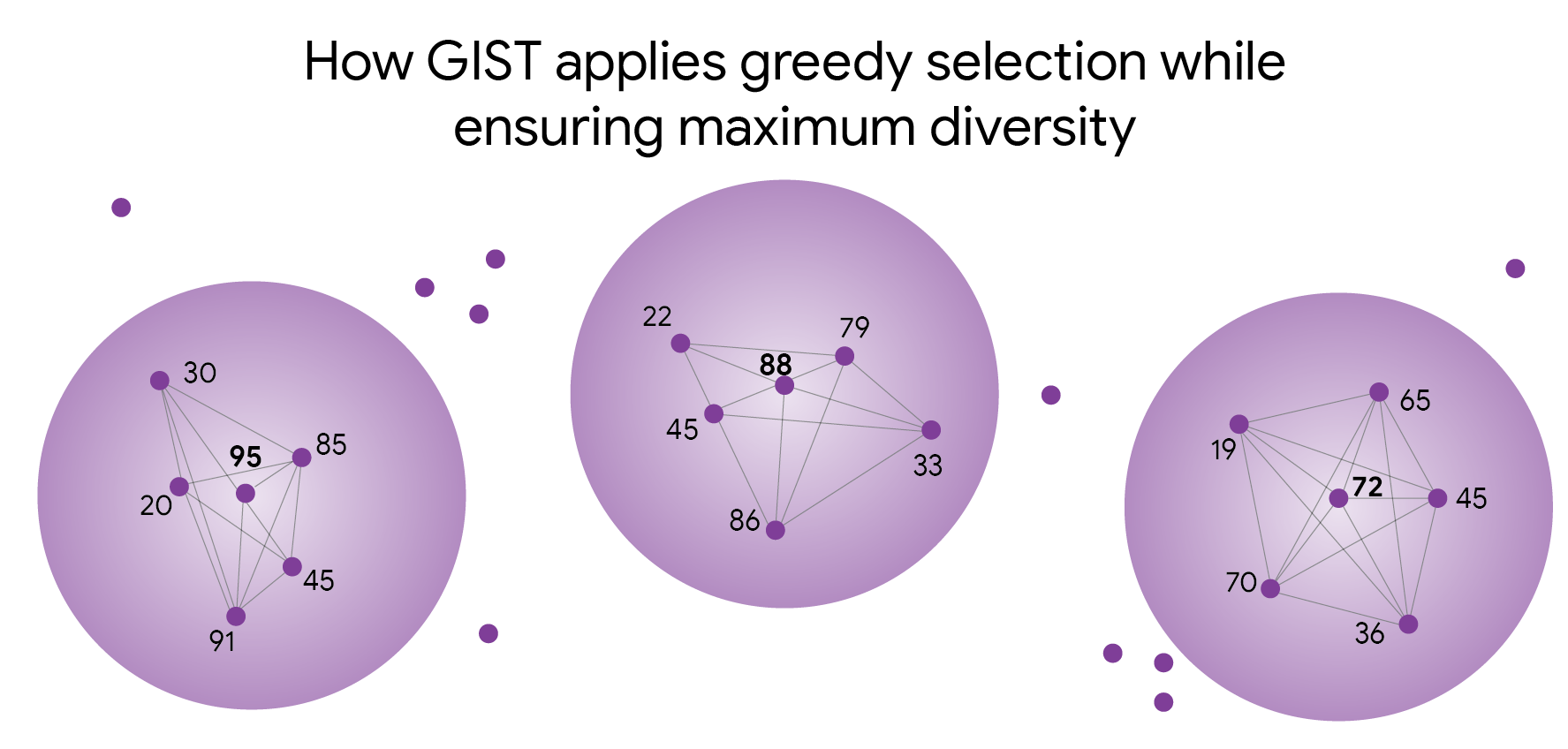
GIST looks for the point with the highest score that isn't already inside someone else's bubble. Then it picks the highest-scoring "VIP" data points (the dots with numbers) and draws a "no-go zone" around them to ensure the final selection is both high-quality and diverse. The higher the number, the more valuable that specific piece of data is for learning.
2. Approximating the independent set
GIST then looks for the maximum-utility subset that can be chosen where no two points are connected in this graph: the classic maximum independent set problem. Imagine planning a dinner party where certain guests can’t sit together. Your goal is to invite the most interesting group of people possible, but you must follow one rule: no two people at the table can have a conflict. This is a massive puzzle because picking one guest might "block" you from inviting three other high-interest people. To find the best combination, you have to check an exponential number of groupings, which is why it is considered one of the hardest problems in computing.
Since the max independent set problem itself is NP-complete (meaning that it’s widely believed there does not exist an efficient algorithm to find the absolute “perfect” answer for a massive dataset) and admits no reasonable approximation algorithm, GIST uses a carefully constructed bicriteria greedy algorithm to approximate the solution efficiently. It iterates through many possible distance thresholds, solving the corresponding independent set problem and ultimately selecting the best solution found across all thresholds. For any minimum distance d achieved by the optimum solution, GIST achieves a comparable utility to the optimum utility at distance threshold d/2.
The bicriteria greedy algorithm acts like a systematic "tuning knob" that finds the right balance between data variety and value. Instead of guessing, it analyzes the actual distances between all data points to create a list of potential spacing rules. It then tests these rules one by one: for each rule, it "greedily" grabs the most valuable points it can find, provided they aren't too close to the points it has already picked. By running this process across every relevant distance and comparing the results, the algorithm identifies the specific "sweet spot" that captures the most useful information while ensuring the data is as spread out as possible.
By cleverly approximating a series of these maximum independent set problems, GIST manages to satisfy the utility goal while respecting the minimum diversity requirement.
Results
Strong guarantees
Our theoretical results are the most significant findings: GIST is the first algorithm to provide a strong, provable guarantee for this diversity-utility tradeoff. The GIST algorithm is guaranteed to find a data subset whose value is at least half the value of the absolute optimal solution (see paper for details). This strong guarantee provides practitioners with a necessary mathematical safety net, ensuring that the algorithm is making an efficient trade-off between maximizing utility while ensuring diversification. Further, we prove that it is NP-hard to find a subset with more than a 0.56 fraction of the optimal value.
Real-world impact
We also evaluated GIST against state-of-the-art benchmarks in various ML applications, focusing on scenarios where diversity and utility are both essential:
- Random: A simple and lightweight approach that promotes diversity in many settings and provides good solutions.
- Margin: Picks data points that the model is currently "uncertain" about and is not incentivized to output a diverse set of training examples.
- k-center: Selects a subset of data points so that every single point in the original, massive dataset is as "close" as possible to one of the selected representatives. Instead of looking for the most important or interesting points, it tries to eliminate "blind spots."
- Submod: Chooses "important" points (utility) while also making sure they aren't "too similar" (diversity). However, it uses a slightly older mathematical way of defining diversity that can sometimes be inconsistent when the dataset becomes large.
We then combined GIST with the other strategies to see if it could make them better.
- GIST-margin: This takes the "picking the hard cases" strategy and forces it to follow GIST's strict diversity rules. It says, "Pick the most confusing examples, but I forbid you from picking two confusing examples that are too similar to each other."
- GIST-submod: Submod uses the GIST framework to handle the diversity part more rigorously than the original submod approach could.
Data sampling for image classification
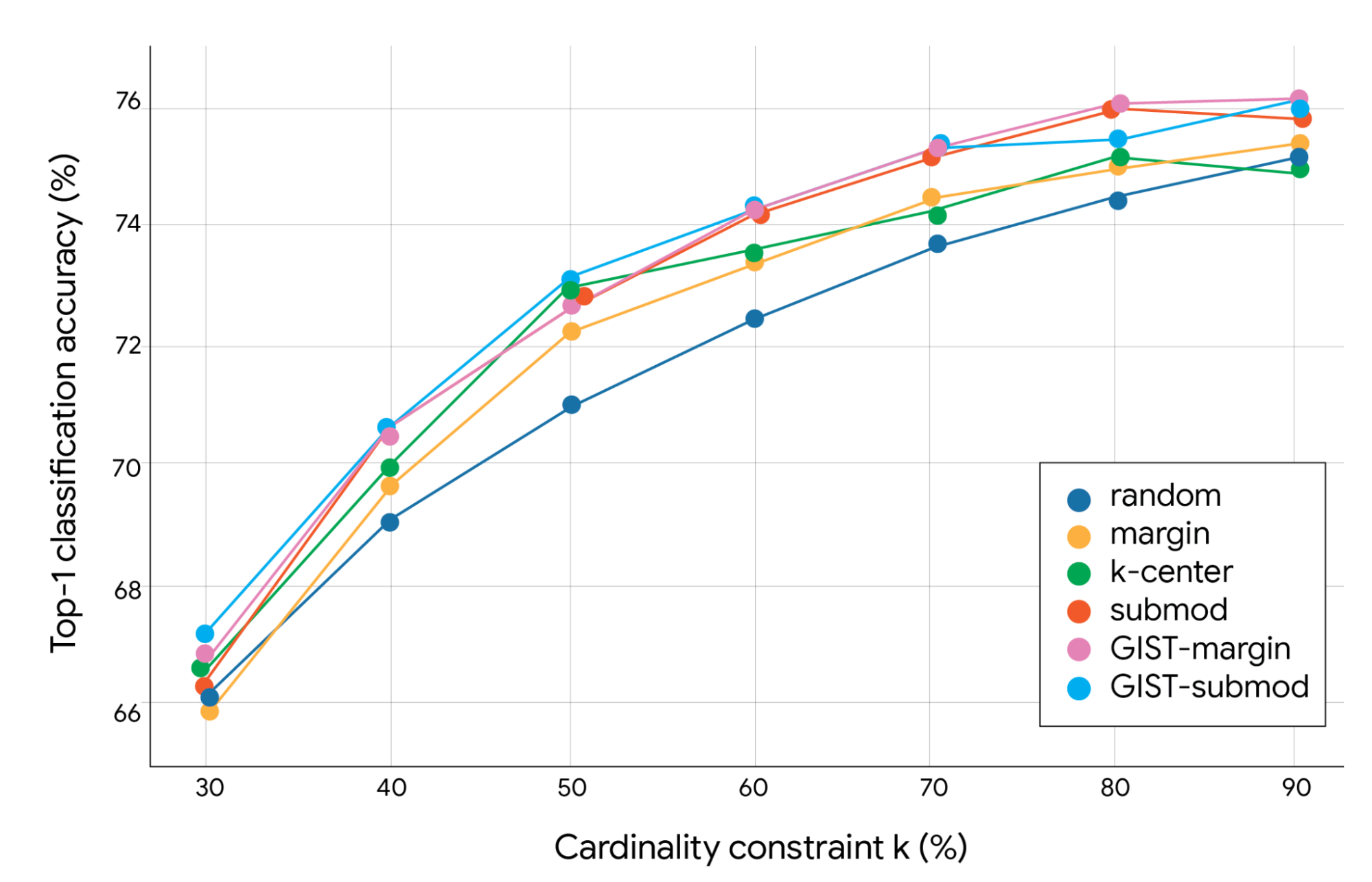
In experiments using a ResNet-56 model on datasets like ImageNet, GIST demonstrated significant advantages in single-shot subset selection. Single-shot data downsampling reduces the volume of a dataset — typically images, signals, or high-dimensional data — in one step while retaining critical information. Unlike iterative or multi-stage processes, this approach maximizes speed and efficiency and is often used to decrease computational burden or to optimize rendering performance in graphics-related tasks.
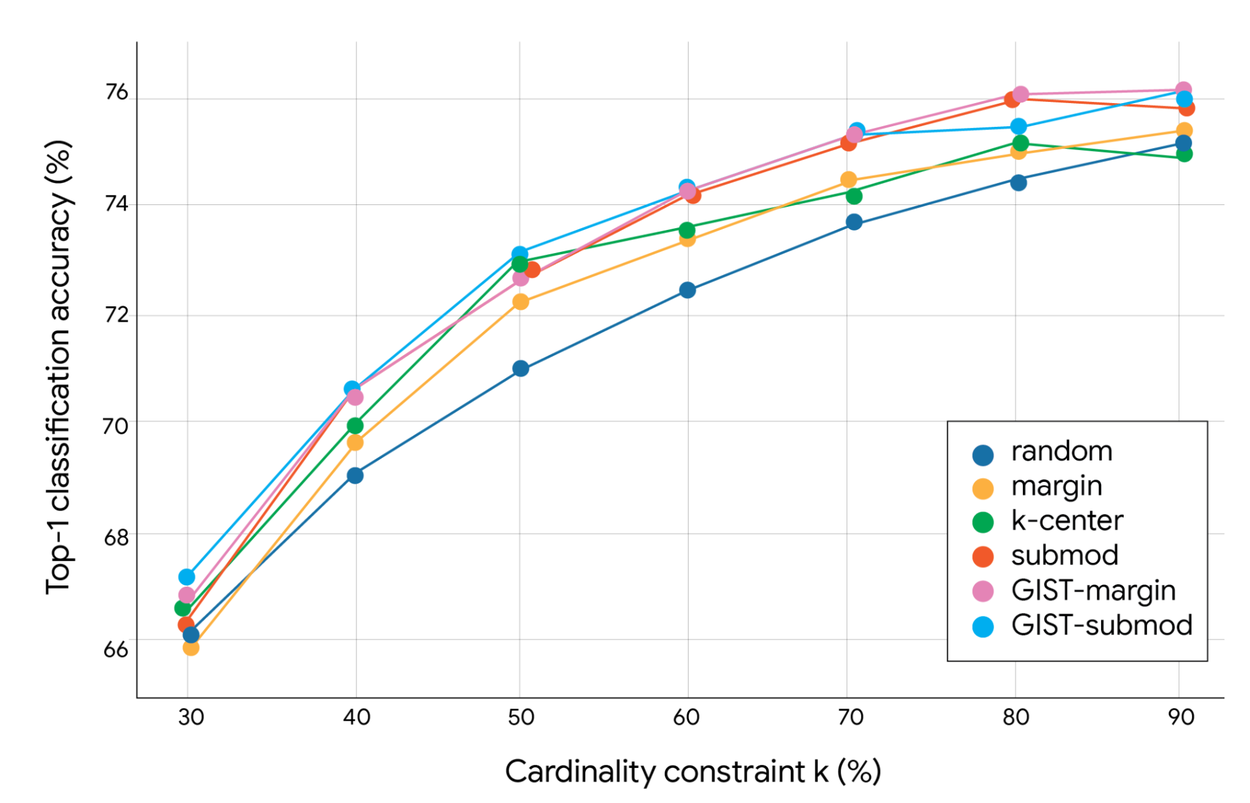
Top-1 classification accuracy (%) of GIST on ImageNet for different single-shot data downsampling algorithms. The cardinality constraint limits the number of items picked. If, for example, there is a pool of 1.3 million images, a cardinality constraint of 10% (k=10%) means that the algorithm is strictly forbidden from picking more than 130,000 images to train the model.
This is critical for data-intensive tasks where we need to select the most informative and diverse images once before beginning costly model training. GIST consistently selected subsets that led to higher model accuracy compared to previous methods, proving its improved ability to balance coverage and non-redundancy.
Running time
Despite the complexity of the underlying problem, the actual subset selection step of GIST is incredibly fast: its running time is often negligible compared to the hours or even days required for training the final ML model. This speed makes GIST practical for integration into large-scale training pipelines with billions of data points.
We also observed the value of the max-min diversity approach with the YouTube Home ranking team, which employed a similar principle to enhance the diversity of video recommendations and consequently improved long-term user value.
Conclusion: A foundation for scalable AI
The challenge of combining competing optimization goals — such as maximizing total utility while maintaining maximum diversity — has been a long-standing hurdle in computational science. The GIST algorithm successfully solves this fundamental trade-off for data selection by providing a single, highly efficient framework.
By breaking the challenging diversity–utility tradeoff problem into a sequence of simpler, approximable tasks, GIST provides the ML community with a provably effective tool. This research establishes a strong foundation for the next generation of scalable AI systems, guaranteeing that as data continues to grow, we can still train models on subsets that are both maximally informative and minimally redundant. The gist of it is, GIST ensures we are sampling data intelligently.
Acknowledgements
We thank Sara Ahmadian from Google Research; Srikumar Ramalingam, Giulia DeSalvo, and Gui Citovsky from Google DeepMind; and Cheenar Banerjee, Cristos Goodrow, Fabio Soldo, and Su-Lin Wu from YouTube who contributed to this work. Matthew Fahrbach, Morteza Zadimoghaddam and Srikumar Ramalingam contributed equally in this research project.