Validating random circuit sampling as a benchmark for measuring quantum progress
October 10, 2024
Kostyantyn Kechedzhi and Alexis Morvan, Research Scientists, Google Quantum AI
We examine random circuit sampling as a method for evaluating quantum computer performance in the presence of noise, specifically their ability to outperform classical supercomputers. This research demonstrates a twofold increase in circuit volume at the same fidelity compared to our 2019 results.
Quick links
While quantum processors in the noisy intermediate-scale quantum (NISQ) era demonstrate remarkable potential, they are susceptible to errors, i.e., noise, that accumulate over time and limit the number of qubits they can effectively handle. This poses a fundamental question: despite the limitations of noise in quantum computing, can these systems still provide practical value and outperform classical supercomputers in specific applications?
In “Phase transitions in random circuit sampling”, published in Nature, we address this question by examining random circuit sampling (RCS) as a method for evaluating the performance of quantum computers in the presence of noise. This research unveils two distinct phase transitions that govern the behavior of quantum computers as noise strength and the number of processor qubits change. Our work reaffirms the reliability of RCS for large-scale experiments, reinforcing its validity as a performance metric for current quantum devices. Our latest results represent a twofold increase in the circuit volume at the same fidelity compared to our 2019 results. Our findings suggest that noisy quantum computers have the potential to outperform supercomputers, even with the current levels of noise. This is a significant step towards developing practical applications for quantum computers.
The significance of RCS
Since we ran our first RCS benchmark in 2019, this approach has emerged as a leading standard for evaluating the progress of quantum computers. It presents a computational task believed to be intractable for classical supercomputers, making it essential for demonstrating quantum advantage, or ‘beyond classical’ capabilities.
The challenge for classical computers lies in the exponential growth of information. As a quantum circuit grows larger, the amount of information required to describe its state increases exponentially. This means that even with complete knowledge of the circuit's design (every gate and their operations) classical computers attempting to fully simulate the circuit or to sample from its output distribution will struggle to keep up.
RCS provides a comprehensive assessment of a device’s quantum circuit volume (a measure that takes into consideration the structure of the circuit and reflects the minimum classical resources needed to simulate it), with a higher value indicating a more powerful computer. Research groups leverage the benchmark to identify where quantum computers might surpass classical supercomputers, even in the presence of noise. The graph below shows the progress of several processor architectures measured using the RCS benchmark. We show the time needed for equivalent computation using the best supercomputer available to get a similar result to the quantum computer both with infinite memory (triangle) and with a parallelizable computation fitting to GPU memory (dot).
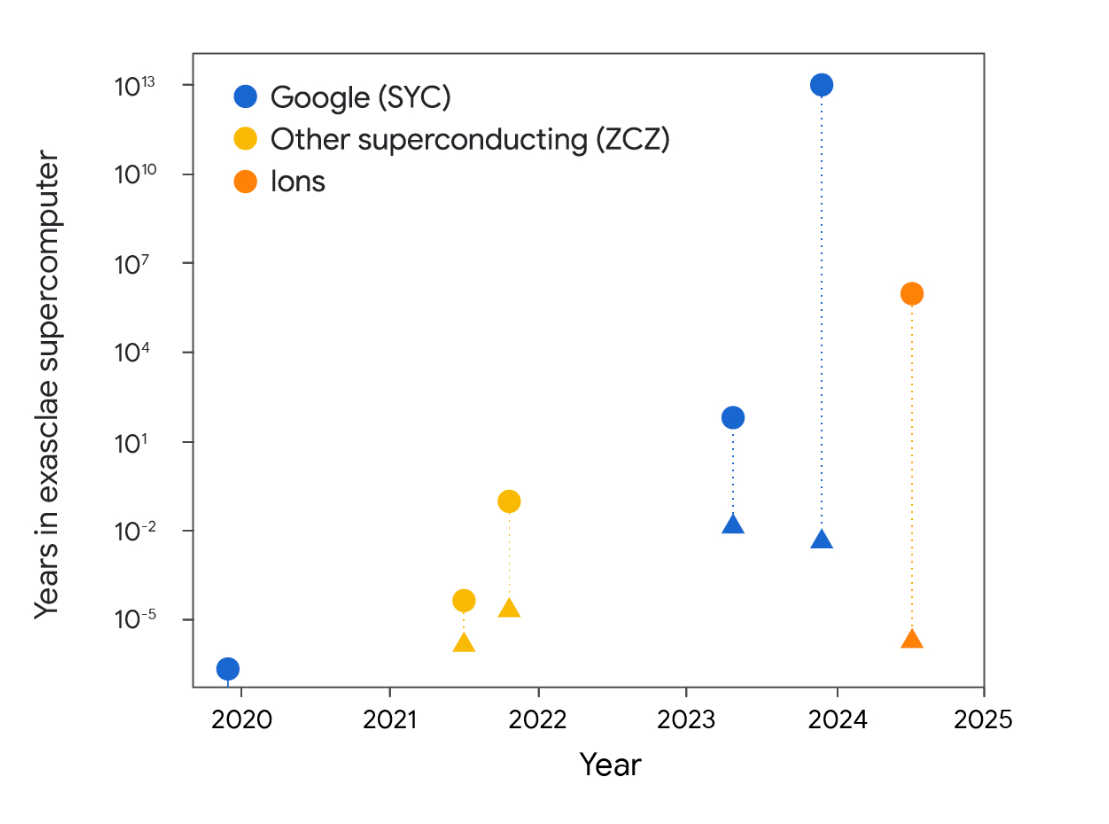
Estimation of the classical compute duration for several RCS experiments. The triangle indicates the classical time needed to sample the RCS distribution under the unrealistic assumption that we have an infinite amount of memory available. The dot indicates the classical time for a parallelizable computation fitting to GPU memory. The colors refer to different processor architectures: “Google (SYC)” refers to the Sycamore processor, “ZCZ” refers to the USTC architecture, and “Ions” refers to Quantinuum.
Verifying the fidelity of RCS
The specific output of RCS benchmarking is an estimate of fidelity, a number between 0 and 1 that characterizes how close the state of the noisy quantum processor is to an ideal noise-free quantum computer implementing the same circuit. Despite the simulation of RCS circuits being beyond the capacity of classical supercomputers, it is possible to obtain an estimate of the fidelity. This is achieved by slightly modifying the circuits to make them amenable to classical computation without inducing a significant change in the value of the fidelity.
The value of fidelity is verified using a technique called patch cross-entropy benchmarking (XEB). For large circuits, this involves dividing the full quantum processor into smaller “patches” and calculating the XEB fidelity for each patch, a computationally feasible task. By multiplying these patch fidelities, an estimation of the overall fidelity of the entire circuit is obtained. In the figure below, the solid lines represent the estimated XEB fidelity based on a digital error model, which captures the noise characteristics of our quantum processor. Our latest experiments within the paper effectively doubled the circuit volume compared to our 2019 beyond classical demonstration while maintaining fidelity. This achievement represents a significant step toward fault-tolerant quantum computing and confirms the feasibility of accessing computationally complex regimes with current noisy quantum devices.
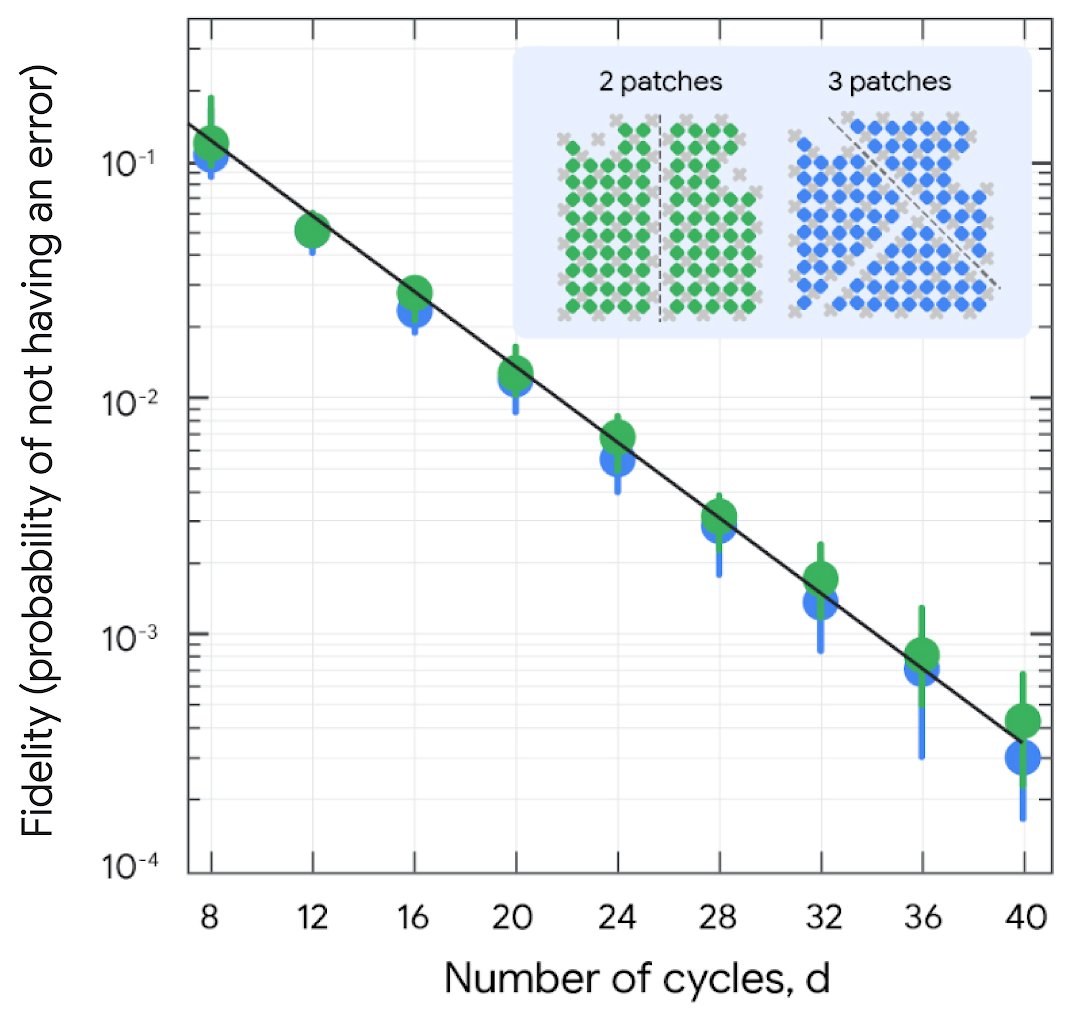
This experiment presents new RCS results with an estimated fidelity of 1.5 × 10-3 at 67 qubits and 32 cycles (circuit depth) or 880 two-qubit gates, which corresponds to more than doubling the circuit volume over previous experiments for the same fidelity. The horizontal axis corresponds to the circuit depth measured in the number of cycles, see quantum circuit diagram for definition.
On phase transitions and spoofing
Noise disrupts quantum correlations, effectively shrinking the available quantum circuit volume. We seek to understand if it’s possible to harness the full quantum circuit volume of a processor despite the effect of noise. In other words, we explore if it would be possible to realize an equivalent computation on a quantum processor of a smaller size.
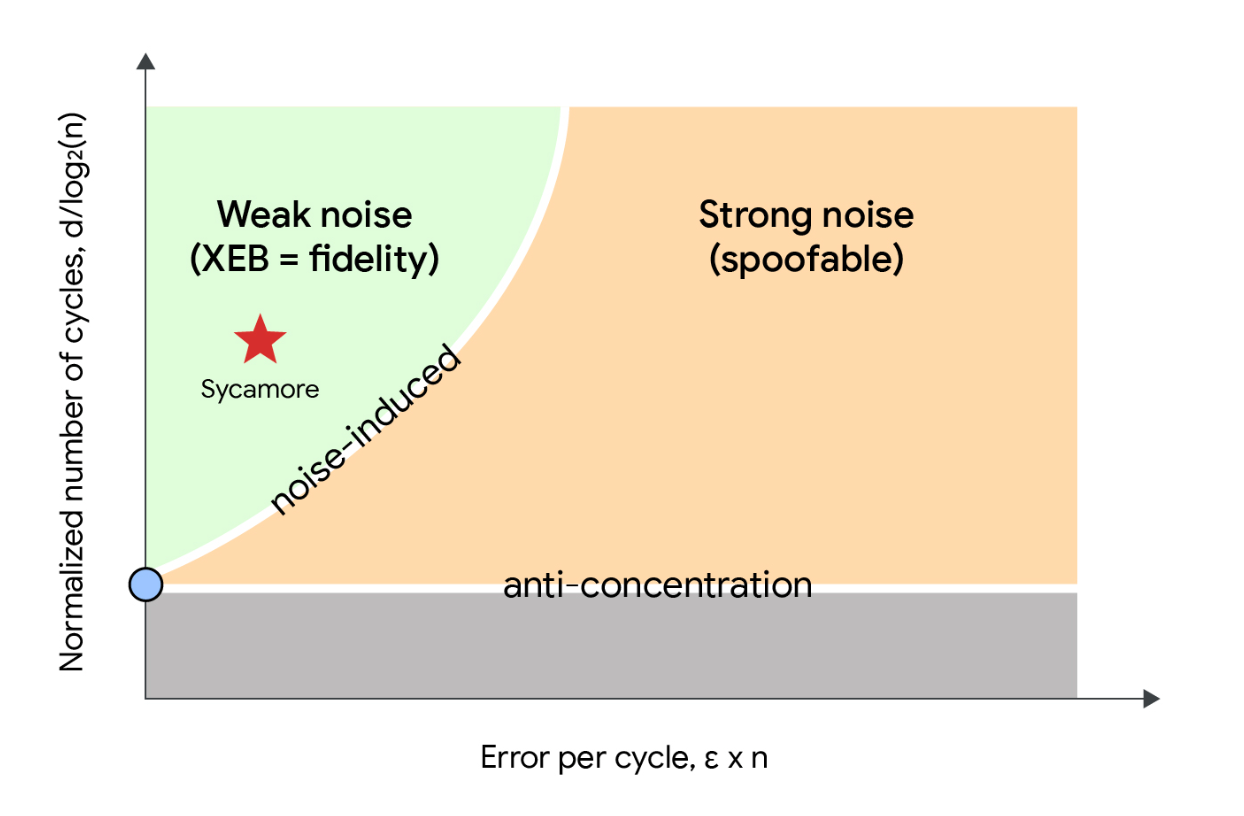
Our research answers this question by revealing regions in the parameter space where the RCS benchmark behaves in a qualitatively different way. These regions (shown in the figure below) are separated by a phase transition. The vertical and horizontal axes correspond to the circuit depth (number of cycles) and error rate per cycle, respectively. In the sufficiently weak noise region (shown in green) quantum correlations extend to the full system, indicating that the quantum computers harness their full computational power. Whereas in the strong noise region (shown in orange) the system may be approximately represented by the product of multiple uncorrelated subsystems, and therefore, a smaller quantum computer could perform an equivalent calculation. In this regime a significant reduction in the cost of classical computation is possible by simulating parts of the system separately.
This is the idea behind spoofing algorithms, which aim to reproduce the RCS benchmark using multiple uncorrelated subsystems instead of the full simulation. Spoofing algorithms crucially rely on the low quantum correlation property of the strong noise regime. Therefore, the existence of the sharp phase transition between the weak and strong noise regions implies that the spoofing algorithms cannot be successful in the weak noise regime.
We employed a three-pronged approach to investigate the phase diagram. First, an analytical model was developed demonstrating the existence of the phase transitions in the large system size limit. Second, extensive numerical simulations were conducted to precisely map out the phase boundaries for our specific quantum hardware. Finally, validation was performed by introducing varying levels of noise into our quantum circuits, observing the transition boundaries experimentally. This multifaceted approach provides compelling evidence for the validity of the phase diagram.
Using numerical simulations we demonstrate that the parameters of our Sycamore processor are well within the low noise regime. In other words, our processor lies firmly in the beyond classical regime, exceeding the capabilities of current supercomputers. This analysis also rules out spoofing algorithms as an efficient method to reproduce our latest RCS benchmark results. The RCS benchmark is a reliable estimator of fidelity in the weak noise regime. The sharp boundary between weak and strong noise regimes provides a clear criterion for ensuring the accuracy of RCS benchmarks.
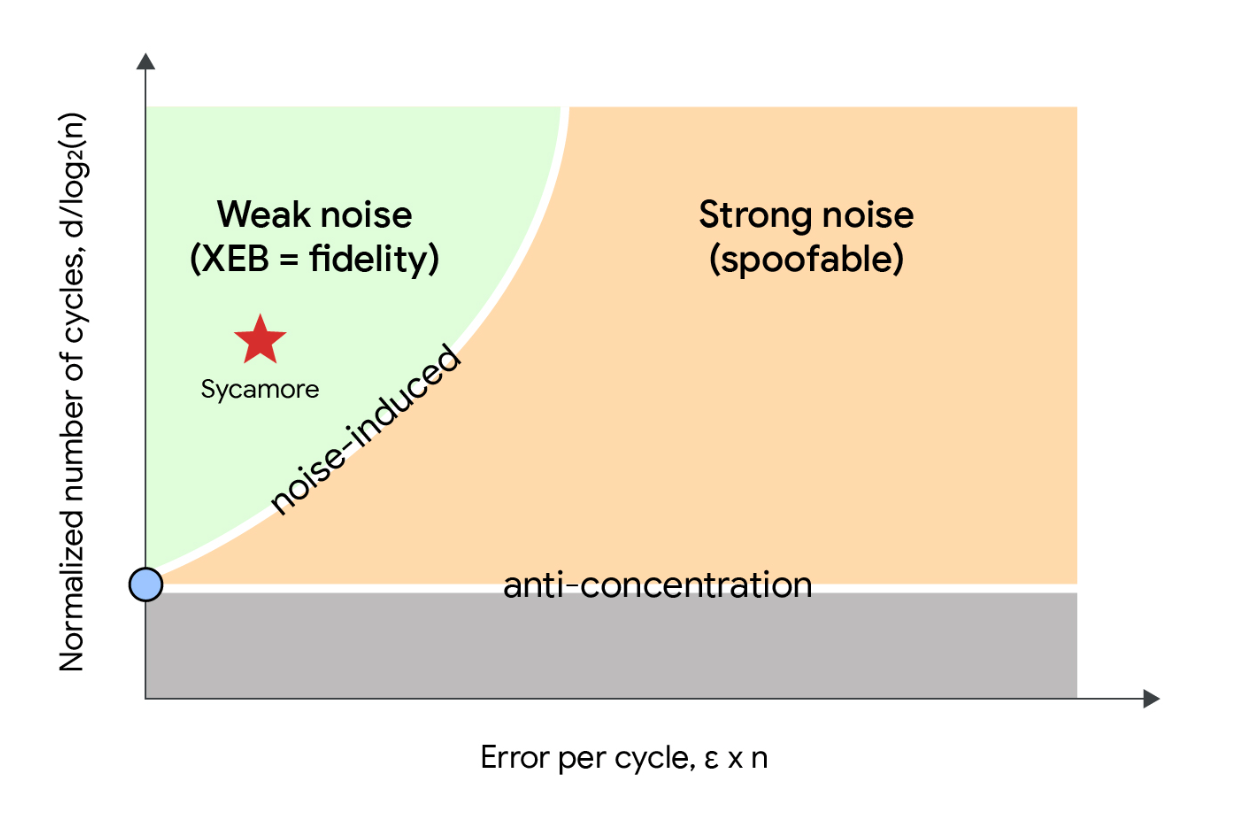
Sketch of the phase diagram. The region labeled “weak noise” in green represents where quantum correlations extend to the full device, enabling beyond classical experiments. In the “strong noise” regime, the system may be approximately represented by the product of multiple uncorrelated subsystems, and the experiment might be spoofable by classical algorithms. The anti-concentration phase transition separates the regimes of a concentrated distribution of output bitstrings and a broad (or anti-concentrated) distribution. In our experiment we identified this transition for noisy RCS circuits.
Phase transitions are fundamental to our understanding of physics, and uncovering a new one in the context of quantum computing is a significant step forward. Moreover, the noise-induced phase transition we demonstrated has unusual properties. In conventional settings the effect of noise is to erode a phase transition to a smooth crossover instead of a transition. Remarkably, in contrast to this conventional behavior, the phase transition we observed in the noisy RCS becomes sharper with increased system size indefinitely despite the presence of noise.
Conclusion and future work
Our work provides a deeper understanding of the nuances of benchmarking of quantum computers. By revealing the phase transition induced by noise, we’ve established clear criteria for ensuring the reliability of these techniques, strengthening the foundation for existing beyond classical claims.
A promising application of quantum computers is to simulate quantum phenomena in nature. Experimental physics and chemistry often rely on measurements of local observables, such as magnetization of a magnet or density of a gas at a particular point in space. Demonstrating quantum algorithms that predict the output of such measurements is the next significant milestone on the path to quantum advantage with real world impact.


