Understanding Transformer reasoning capabilities via graph algorithms
December 20, 2024
Clayton Sanford and Bahar Fatemi, Research Scientists, Google Research
We provide a comprehensive evaluation of transformer models’ graph reasoning capabilities and demonstrate that they often outperform more domain-specific graph neural networks.
Quick links
Transformers are a general purpose sequential deep learning architecture introduced by Google in 2017. They have recently, and surprisingly, hinted at being good at learning graph-based algorithmic tasks like connectivity (e.g., “Is there a path from node A to node B?”), shortest path (“How many edges must one take to get from node A to node B?”), and cycle checks (“Is there a cycle in the graph, e.g., edges from A → B, B → C, C → A?”).
Why is this surprising? Because unlike message passing neural networks (MPNNs), whose parameters are explicitly encoded with the structure of the input graphs, transformers are a general purpose architecture best-known for language tasks. Their backbone is a computationally expensive self-attention mechanism that encodes associations between input words/tokens and is not explicitly designed for graphs. So, while transformer-based neural networks have made tremendous empirical advances, we clearly still lack a theoretical understanding of their algorithmic reasoning capabilities in realistic scenarios. Knowing which architecture is best for which real-world tasks means spending a lot less time defining and evaluating new architectures via hand-picked tasks and a much better understanding of architectural decision trade-offs.
In “Understanding Transformer Reasoning Capabilities via Graph Algorithms”, we conduct an extensive study of graph reasoning problems with transformers from both theoretical and empirical perspectives. We find that transformers can solve parallelizable tasks (like connectivity) in a highly parameter-efficient manner and outperform graph neural networks (GNNs) on tasks that require the analysis of long-range dependencies. We also introduce a novel representational hierarchy of graph reasoning tasks that formalizes reasoning capabilities of transformers in several realistic parameter scaling regimes.
Experiment
MPNNs are a bespoke neural architecture explicitly designed to learn functions that respect graph structures, while transformers are much more generic. But transformers and MPNNs can be trained to solve graph algorithmic problems using similar ML frameworks.
For the empirical part of the experiment, we investigated if a transformer could encode graph tasks the way MPNNs do, and if so, do it more efficiently.
To test this, we encoded a graph task as a transformer input. Given a graph instance (with nodes and edges) and a query (determine whether nodes 𝑣2 and 𝑣4 are connected), we encoded each node ID as a discrete token (similarly to how LLMs map words to tokens) and each edge as a pair of tokens. We then encoded the problem as a list of node tokens, a list of edge tokens, and a token encoding of the query.
How a graph reasoning task instance (here, graph connectivity) is embedded as a transformer input.
Seeing as transformers and MPNNs are not the only ML approaches for the structural analysis of graphs, we also compared the analytical capabilities of a wide variety of other GNN- and transformer-based architectures. For GNNs, we compared both transformers and MPNNs to models like graph convolutional networks (GCNs) and graph isomorphism networks (GINs).
Additionally, we compared our transformers with much larger language models. Language models are transformers as well, but with many orders of magnitude more parameters. We compared transformers to the language modeling approach described in Talk Like a Graph, which encodes the graph as text, using natural language to describe relationships instead of treating an input graph as a collection of abstract tokens.
We asked a trained language model to solve various retrieval tasks with a variety of prompting approaches:
- Zero-shot, which provides only a single prompt and asks for the solution without further hints.
- Few-shot, which provides several examples of solved prompt–response pairs before asking the model to solve a task.
- Chain-of-thought (CoT), which provides a collection of examples (similar to few-shot), each of which contains a prompt, a response, and an explanation before asking the model to solve a task.
- Zero-shot CoT, which asks the model to show its work, without including additional worked-out examples as context.
- CoT-bag, which asks the LLM to construct a graph before being provided with relevant information.
For the theoretical part of the experiment, we created a task difficulty hierarchy to assess which tasks transformers can solve with small models.
We only considered graph reasoning tasks that apply to undirected and unweighted graphs of bounded size: node count, edge count, edge existence, node degree, connectivity, node connectivity (for undirected graphs), cycle check, and shortest path.
In this hierarchy, we categorized graph task difficulty based on depth (the number of self-attention layers in the transformer, computed sequentially), width (the dimension of the vectors used for each graph token), number of blank tokens, and three different types:
- Retrieval tasks: easy, local aggregation tasks.
- Parallelizable tasks: tasks that benefit greatly from parallel operations.
- Search: tasks with limited benefits from parallel operations.
Results
Empirical
For small models (~60M parameters) trained on specialized data, transformers outperform much larger LLMs without targeted training (as shown in the bar chart below). Also, their algorithmic reasoning capabilities can be enhanced with few samples and few parameters.
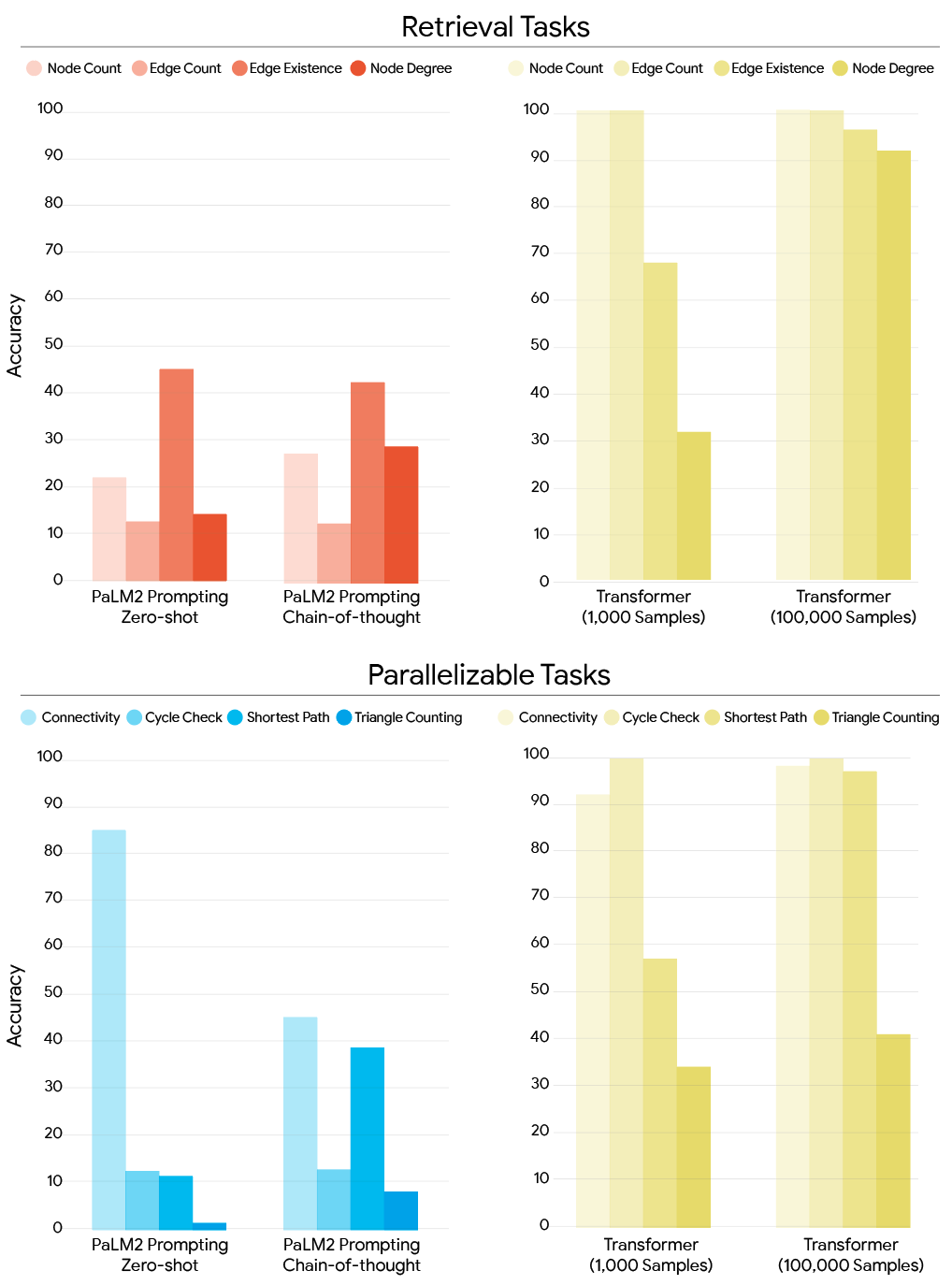
Accuracy on all retrieval tasks (top) and parallelizable and search tasks (bottom) by mode of training, contrasting prompted PaLM2 LLMs (left) and trained transformers (right).
As shown below, MPNNs perform better on “local” tasks, where we aggregate information about neighboring nodes without needing to make many “hops” of reasoning. Whether trained on 1K or 100K samples, MPNNs have higher accuracies on local tasks like node degree (the maximum number of edges adjacent to a node) and cycle check.
Moreover, transformers perform better on “global” tasks, where information needs to be propagated across the graph instances. An example of a global task would be graph connectivity, because any two nodes might be far apart in a graph.
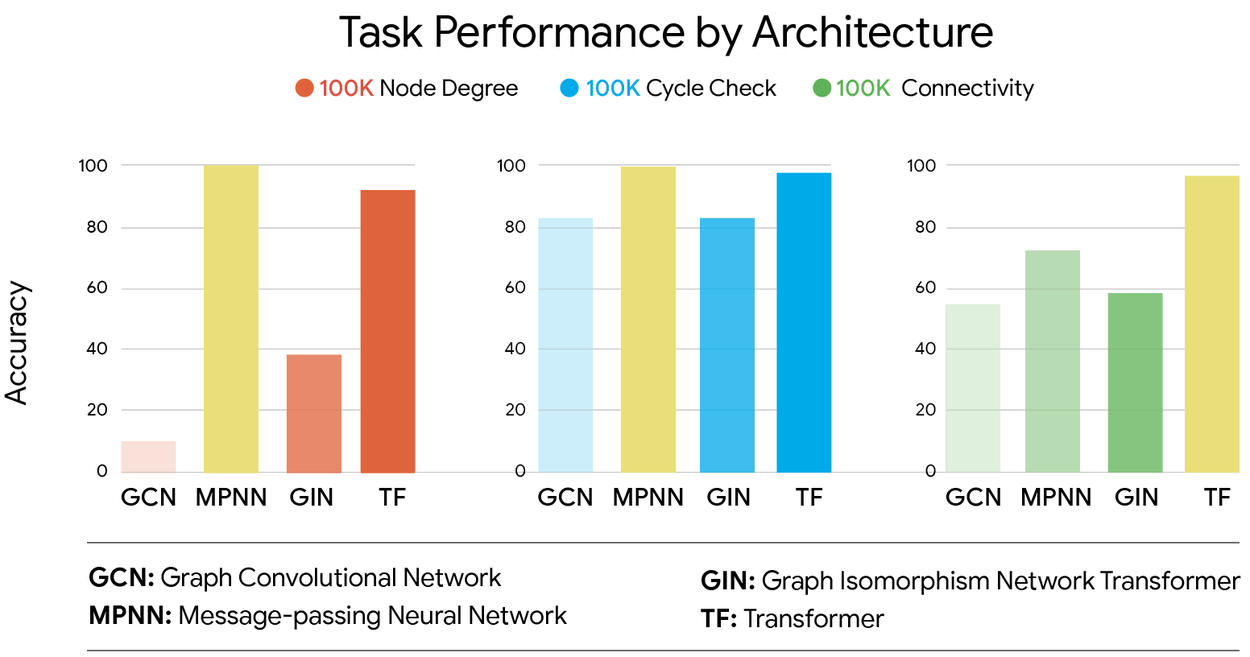
Task performance by architecture, comparing node degree to cycle check to connectivity.
These results show that the difference between the small sample regime and the large sample regime is much greater for transformers, and that GNNs don't come close to transformer performance when trained on 100K samples.
There are two key dynamics at play when training neural networks: capacity and learnability. Capacity represents the fundamental limit of a neural network architecture. That is, capacity governs what kinds of mathematical functions can be represented by a neural architecture. Learnability asks whether these functions can actually be learned in an ML setting with a relatively small number of training samples. We say that an architecture has a positive inductive bias for certain kinds of solutions if it tends to gravitate towards them with few samples.
If we try to understand our transformer and MPNN results under this framework, we see that GNNs indeed have better inductive biases for graph tasks, as is evident by their superior performance in less data-rich environments. On the other hand, the success of the transformers on larger datasets indicates that GNNs may be limited by capacity, since those reflect fundamental model shortcomings that cannot be overcome with more data.
Theoretical
We supported the empirical results with theoretical results that contrast the capacity, or expressivity, of the two architectures. Prior work has shown that transformers can simulate parallel algorithms, while other models like MPNNs are limited by their lack of global connections. Using our task difficulty hierarchy, we showed that transformers have a much greater expressivity for parallelizable tasks under the MPC model and can solve them using logarithmic depth and bounded width (that is, the width of the model is at most some quantity m that grows much slower than the number of graph tokens N, i.e. m ≤ N0.1). On the other hand, no MPNN can solve these tasks unless they are much larger both computationally and in terms of parameter count.
We also found that retrieval tasks are solvable with a single-layer transformer model, and parallelizable tasks can be done easily with log depth (i.e., the depth of the transformer scales logarithmically with number of nodes in the graph). Search tasks can also be done with log depth, but not in a parameter-efficient way.
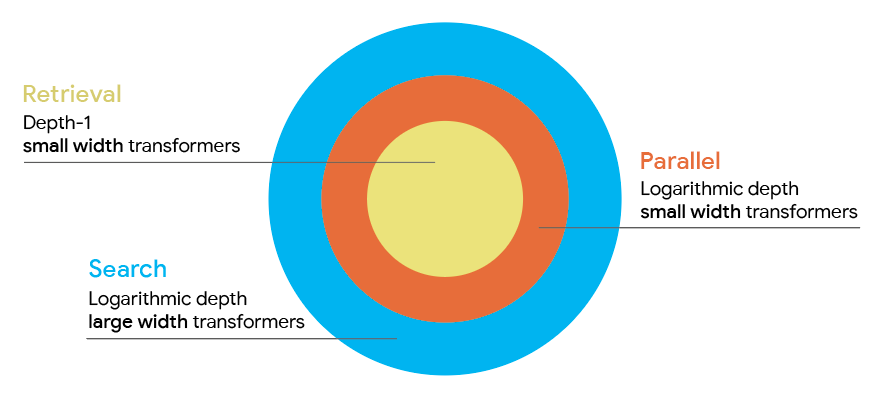
A visualization of the task difficulty hierarchy, where retrieval, parallel, and search tasks are organized based on the complexity of the transformers needed to solve them.
These results suggest why transformers perform so much better on connectivity — unlike GNNs, the size of the model (in terms of depth and number of parameters) does not need to grow rapidly with the size of the input graph.
Conclusion
We provide a comprehensive evaluation of transformer models’ graph reasoning capabilities, shedding light on their effectiveness across diverse graph reasoning tasks. By introducing a novel representational hierarchy, the study distinguishes between retrieval, parallelizable, and search reasoning tasks and offers insights into the performance of transformers at varying levels of granularity. The empirical investigation reveals that transformers exhibit strong performance in graph-based reasoning problems, often matching or surpassing specialized graph models. Furthermore, the study highlights transformers’ exceptional ability to capture global graph patterns effectively, showcasing their capability in understanding long-range dependencies, a critical factor in solving tasks involving global graph structures. Overall, this work crystallizes precise representational trade-offs that reflect the fundamental reasoning capabilities of transformers and demonstrates that the tasks used to quantify those capabilities are indeed learnable in a sample-efficient and parameter-efficient manner.
Acknowledgments
This work was done in collaboration with colleagues across Google, including Ethan Hall, Anton Tsitsulin, Mehran Kazemi, Bryan Perozzi, Jonathan Halcrow, and Vahab Mirrokni.





