Towards an exact (quantum) description of chemistry

“...nature isn't classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical...” - Richard Feynman, Simulating Physics with Computers

One of the most promising applications of quantum computing is the ability to efficiently model quantum systems in nature that are considered intractable for classical computers. Now, in collaboration with the Aspuru-Guzik group at Harvard and researchers from Lawrence Berkeley National Labs, UC Santa Barbara, Tufts University and University College London, we have performed the first completely scalable quantum simulation of a molecule. Our experimental results are detailed in the paper Scalable Quantum Simulation of Molecular Energies, which recently appeared in Physical Review X.

The goal of our experiment was to use quantum hardware to efficiently solve the molecular electronic structure problem, which seeks the solution for the lowest energy configuration of electrons in the presence of a given nuclear configuration. In order to predict chemical reaction rates (which govern the mechanism of chemical reactions), one must make these calculations to extremely high precision. The ability to predict such rates could revolutionize the design of solar cells, industrial catalysts, batteries, flexible electronics, medicines, materials and more. The primary difficulty is that molecular systems form highly entangled quantum superposition states which require exponentially many classical computing resources in order to represent to sufficiently high precision. For example, exactly computing the energies of methane (CH₄) takes about one second, but the same calculation takes about ten minutes for ethane (C₂H₆) and about ten days for propane (C₃H₈).

In our experiment, we focus on an approach known as the variational quantum eigensolver (VQE), which can be understood as a quantum analog of a neural network. Whereas a classical neural network is a parameterized mapping that one trains in order to model classical data, VQE is a parameterized mapping (e.g. a quantum circuit) that one trains in order to model quantum data (e.g. a molecular wavefunction). The training objective for VQE is the molecular energy function, which is always minimized by the true ground state. The quantum advantage of VQE is that quantum bits can efficiently represent the molecular wavefunction whereas exponentially many classical bits would be required.

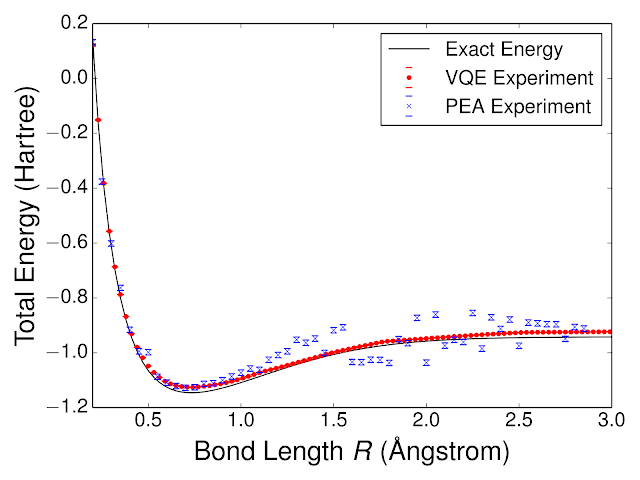
Using VQE, we quantum computed the energy landscape of molecular hydrogen, H₂. We compared the performance of VQE to another quantum algorithm for chemistry, the phase estimation algorithm (PEA). Experimentally computed energies, as a function of the H - H bond length, are shown below alongside the exact curve. We were able to obtain such high performance with VQE because the neural-network-like training loop helped to establish experimentally optimal circuit parameters for representing the wavefunction in the presence of systematic control errors. One can understand this by considering a hardware implementation of a neural network with a faulty weight, e.g. the weight is only represented half as strong as it should be. Because the weights of the neural network are established via a closed-loop training procedure which can compensate for such systematic errors, the hardware neural network is robust against such imperfections. Likewise, despite systematic errors in our implementation of the VQE circuit, we are still able to learn an accurate model for the wavefunction. This robustness inspires hope that VQE may be able to solve classically intractable problems without quantum error correction.
While the energies of molecular hydrogen can be computed classically (albeit inefficiently), as one scales up quantum hardware it becomes possible to simulate even larger chemical systems, including classically intractable ones. For instance, with only about a hundred reliable quantum bits one could model the process by which bacteria produce fertilizer at room temperature. Elucidating this mechanism is a famous open problem in chemistry because the way humans produce fertilizer is extremely inefficient and consumes 1-2% of the world's energy annually. Such calculations could also assist with breakthroughs in fundamental science, for instance, in the understanding of high temperature superconductivity.

Though many theoretical and experimental challenges lay ahead, a quantum enabled paradigm shift from qualitative / descriptive chemistry simulations to quantitative / predictive chemistry simulations could modernize the field so dramatically that the examples imaginable today are just the tip of the iceberg.