Scheduling in a changing world: Maximizing throughput with time-varying capacity
February 11, 2026
Manish Purohit, Research Scientist, Google Research
We introduce new, provably effective algorithms for scheduling jobs without interruptions on cloud infrastructure when machine availability constantly fluctuates.
Quick links
In the world of algorithmic job scheduling, computing resources are often viewed as static: a server has a fixed number of CPUs, or a cluster has a constant number of available machines. However, the reality of modern large-scale cloud computing is far more dynamic. Resources fluctuate constantly due to hardware failure, maintenance cycles, or power limitations.
More significantly, in tiered scheduling systems, high-priority tasks often claim resources on demand, leaving a time-varying amount of “leftover” capacity for lower-priority batch jobs. Imagine a restaurant where tables are reserved for VIPs at different times; scheduling regular customers on the remaining tables can become a complex puzzle.
When these low-priority jobs are non-preemptive — meaning they cannot be paused and resumed later — the stakes are high. If a job is interrupted because capacity drops, all progress is lost. The scheduler must decide: Do we start this long job now, risking a future capacity drop? Or do we wait for a safer window, potentially missing the deadline?
In “Non-preemptive Throughput Maximization under Time-varying Capacity”, presented at SPAA 2025, we initiate the study of maximizing throughput (total weight or number of successful jobs) in environments when the available capacity fluctuates over time. Our research provides the first constant-factor (i.e., the "gap" between the algorithm's answer and the optimal answer is guaranteed to be a fixed, stable number, regardless of how large the problem gets) approximation algorithms for several variants of this problem, offering a theoretical foundation for building more robust schedulers in volatile cloud environments.
Defining the scheduling problem
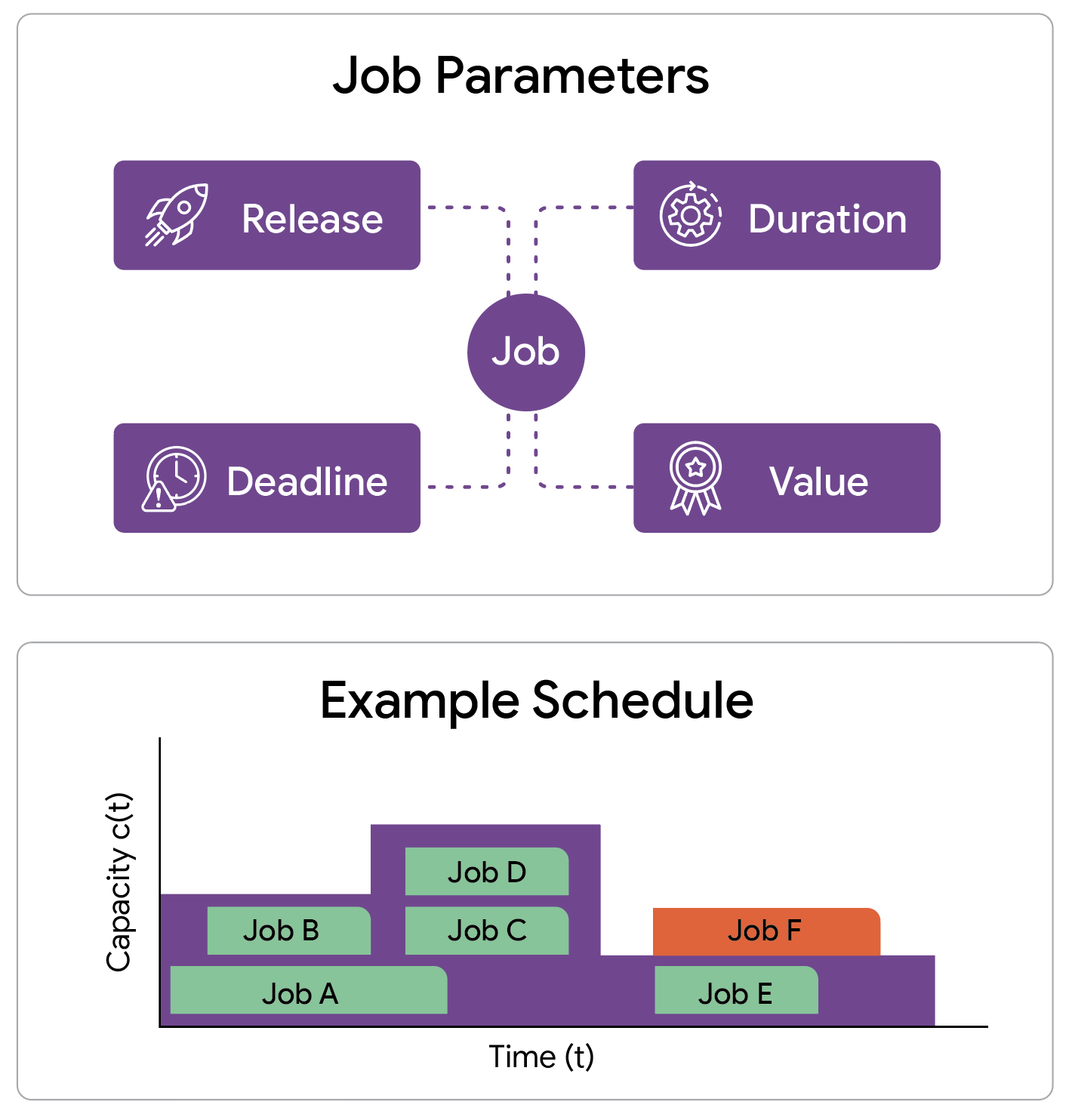
Our work focuses on designing a scheduling model that captures a number of key constraints. We consider a single machine (or cluster) with a capacity profile that varies over time. This profile dictates the maximum number of jobs that can run in parallel at any given moment. We are given a collection of potential jobs, each characterized by four key attributes:
- Release time: When the job becomes available to run
- Deadline: A hard deadline by which the job must finish
- Processing time: The duration for which the machine must work on the job
- Weight: The value gained if the job is successfully completed
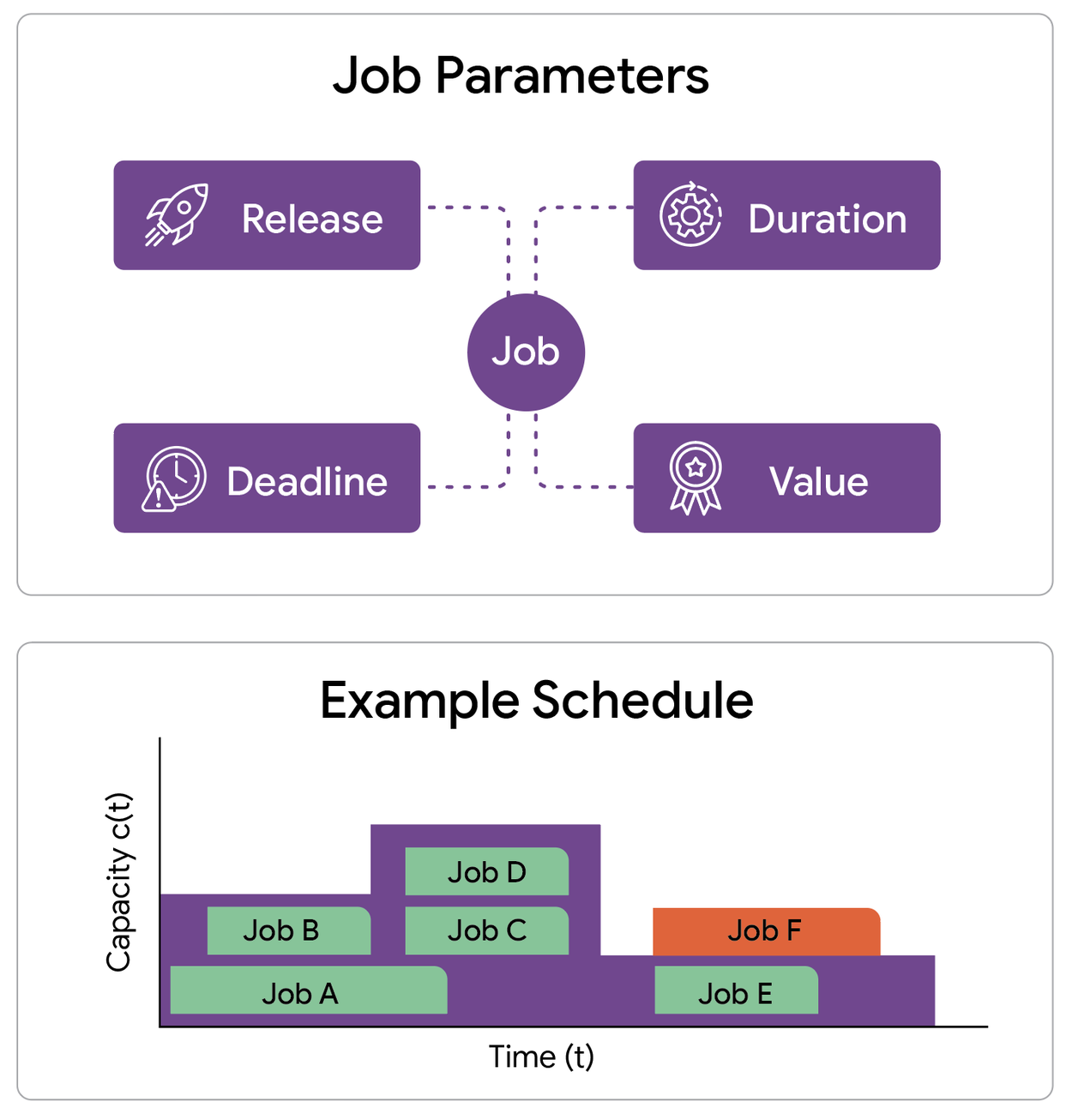
An instance of throughput maximization problem consists of a set of jobs, each with its release time, deadline, duration and value, and a capacity profile for the machine. The capacity profile determines the maximum number of jobs that can be processed simultaneously at any given time.
The goal is to select a subset of jobs and schedule them so that each selected job runs continuously within its valid window. The critical constraint is that any time, the total number of running jobs must not exceed the current capacity. Our objective is to maximize the throughput, i.e., the total weight of all completed jobs.
We address this problem in two distinct environments:
- Offline: Where future job arrivals and capacity changes are known in advance.
- Online: Where jobs arrive in real time, and the scheduler must make irrevocable decisions without knowledge of future arrivals. The capacity landscape is still known in advance.
Results for the offline setting
In the offline setting, where we can plan ahead, we find that simple strategies perform surprisingly well. Because finding the optimal schedule in this setting is considered “NP-hard” (i.e., there is no known shortcut to find the perfect answer), we focus on algorithms with rigorous approximation guarantees. We analyze a myopic strategy, called Greedy, that iteratively schedules the job that would finish earliest and prove that this simple heuristic achieves a 1/2-approximation (in this context, often as good as it gets) when jobs have unit profits. This means that even in the worst-case scenario with adversarially chosen jobs and capacity profiles, our simple algorithm is guaranteed to schedule at least half of the optimal number of jobs. This matches the guarantees enjoyed by Greedy on simpler, unit capacity machines that can only do one task at a time. When different jobs can have different associated profits, we utilize a primal-dual framework to achieve a 1/4-approximation.
Results for the online setting
The real complexity lies in the online setting, where jobs arrive dynamically and the scheduler must make immediate, irrevocable decisions without knowing what jobs will arrive next. We quantified the performance of an online algorithm via its competitive ratio, which is the worst case comparison between the throughput of our online algorithm and the throughput of an optimal algorithm that is aware of all the jobs apriori.
The standard non-preemptive algorithms fail completely here as their competitive ratio approaches zero. This happens because a single bad decision of scheduling a long job can ruin the possibility of scheduling many future smaller jobs. In this example, if you imagine that each completed job brings equal weight, regardless of its length, completing many short jobs is much more profitable than completing one long job.
To make the online problem solvable and reflect real-world flexibility, we studied two models that allow an active job to be interrupted if a better opportunity arises (though only jobs restarted and later completed non-preemptively count as successful).
Interruption with restarts
In this model, an online algorithm is allowed to interrupt a currently executing job. While the partial work already performed on the interrupted job is lost, the job itself remains in the system and can be retried.
We found that the flexibility provided by allowing job restarts is highly beneficial. A variant of Greedy that iteratively schedules the job that finishes earliest continues to achieve a 1/2-competitive ratio, matching the result in the offline setting.
Interruption without restarts
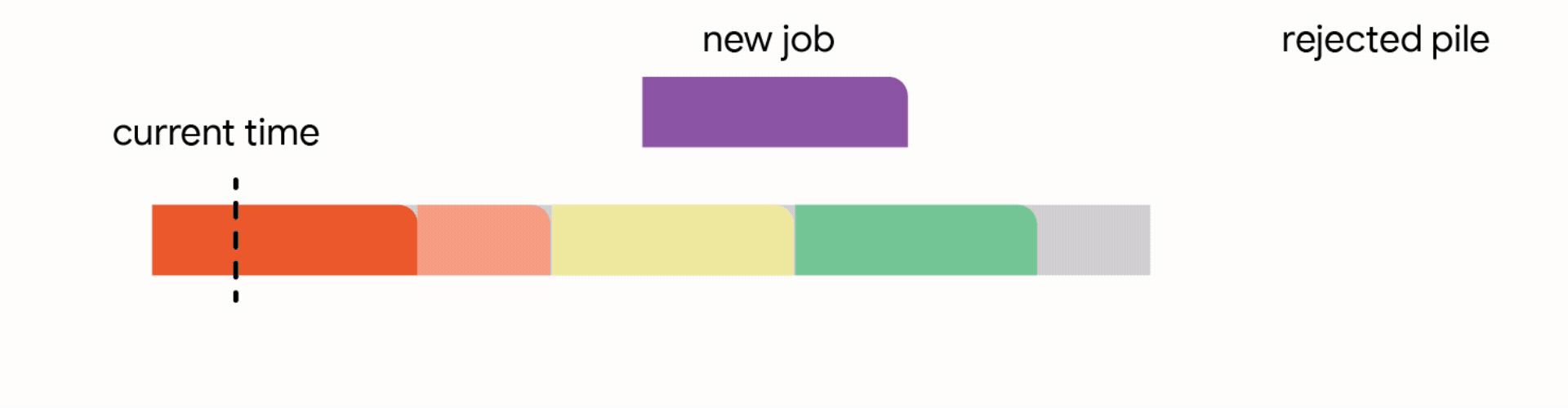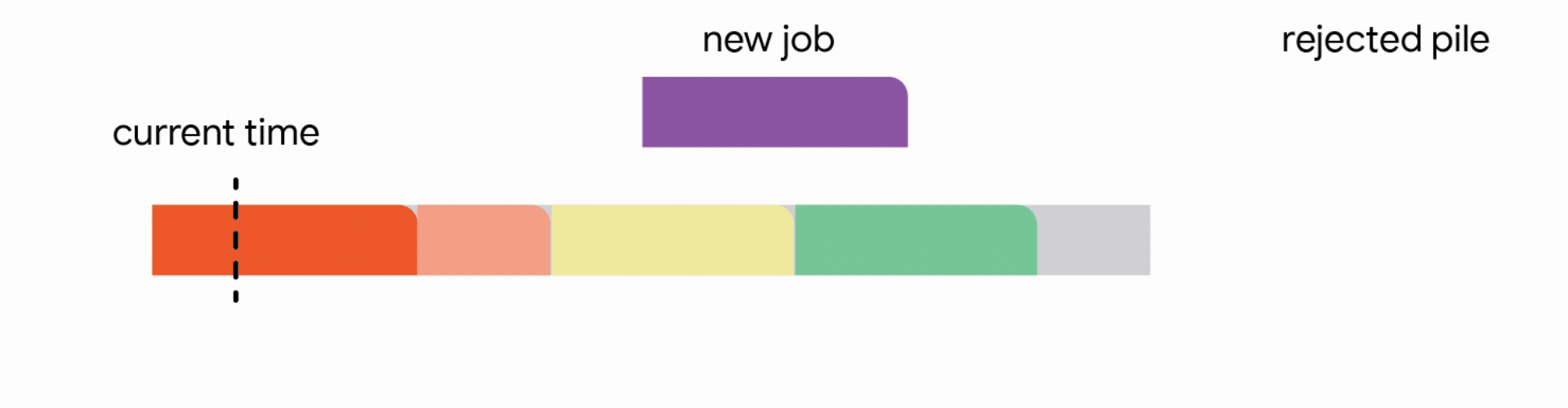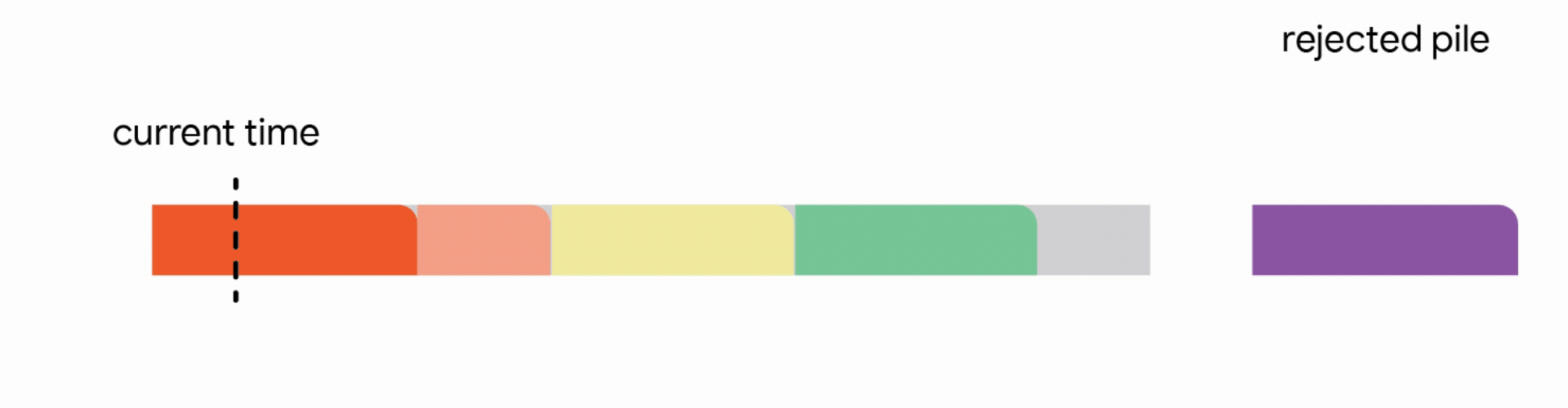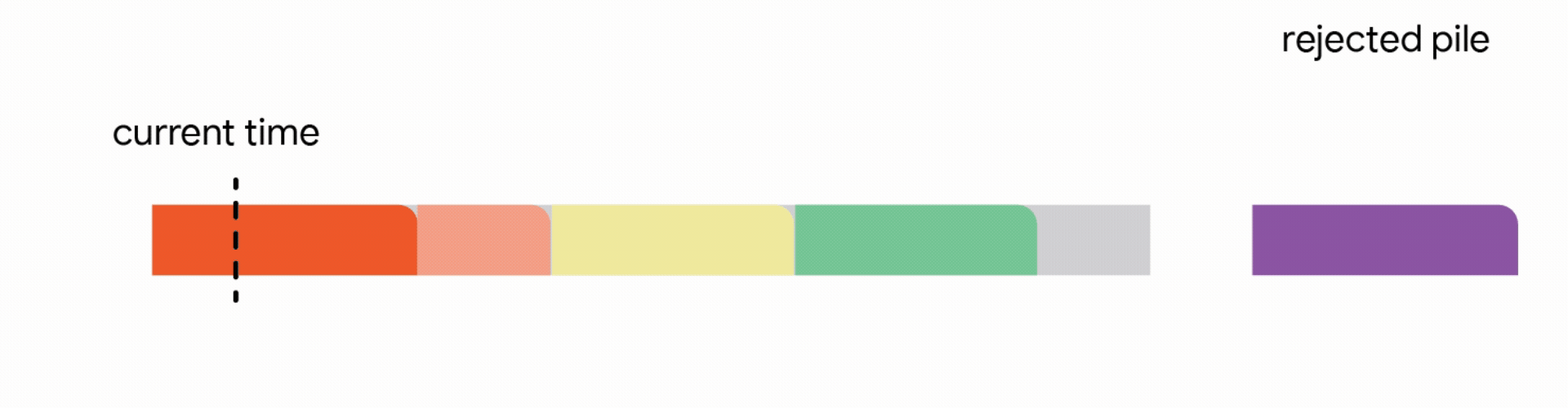
In this stricter model, all work performed on the interrupted job is lost and the job itself is discarded forever. Unfortunately, we find that in this strict model, any online algorithm can encounter a sequence of jobs that forces it into decisions which prevent it from satisfying much more work in the future. Once again, the competitive ratio of all online algorithms approaches zero. Analyzing the above hard instances led us to focus on the practical scenario where all jobs share a common deadline (e.g., all data processing must finish by the nightly batch run). For such common deadline instances, we devise novel constant competitive algorithms. Our algorithm is very intuitive and we describe the algorithm here for the simple setting of a unit capacity profile, i.e., we can schedule a single job at any time.
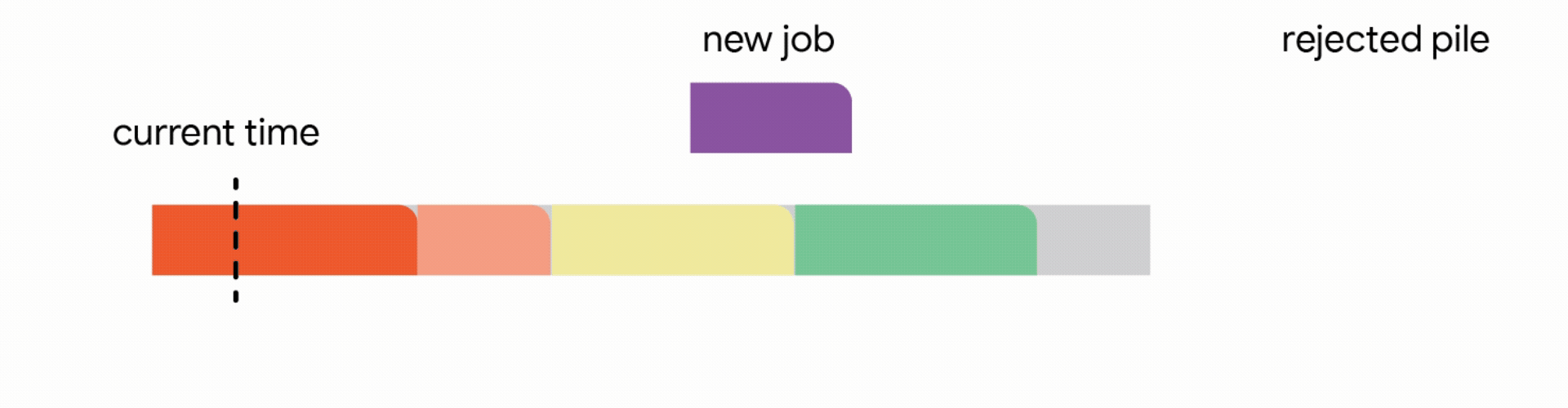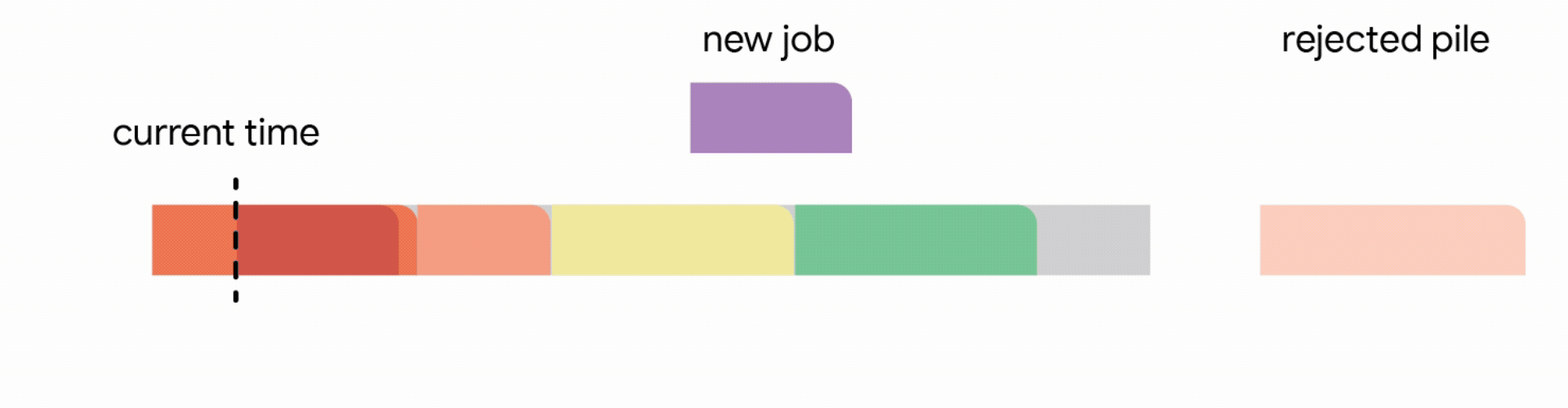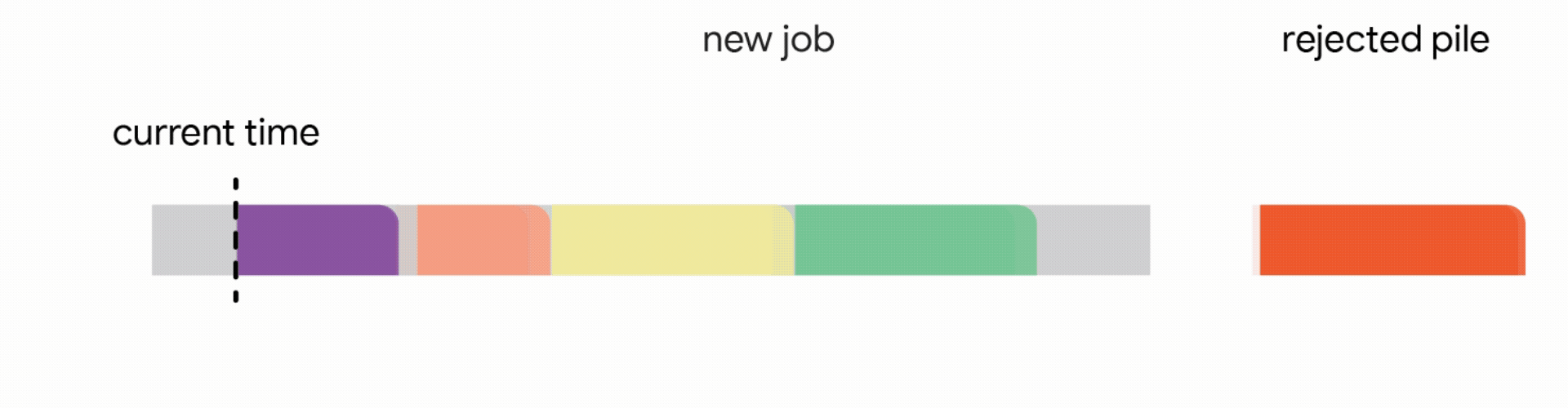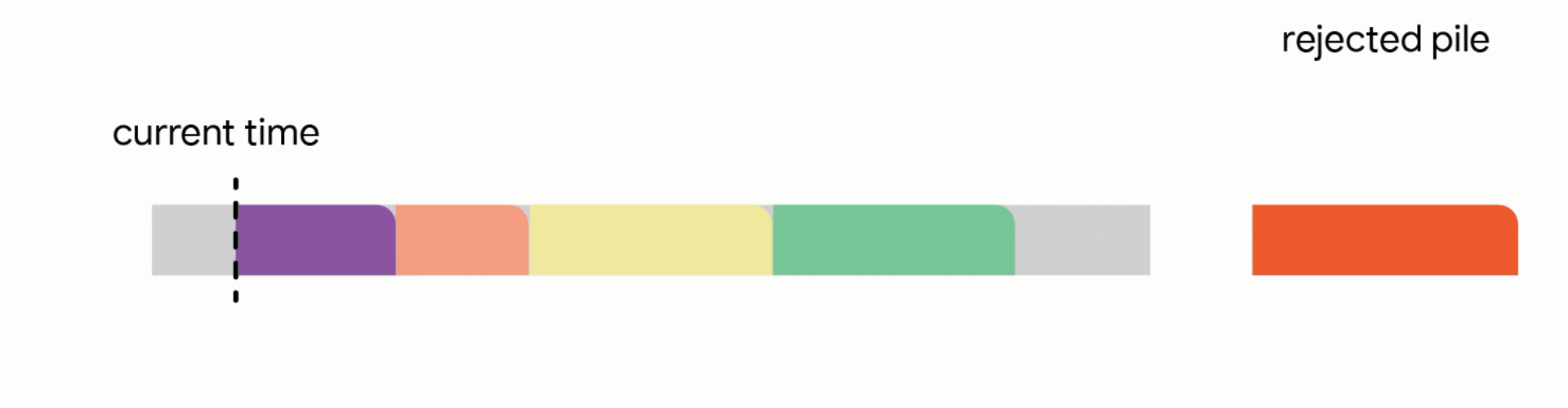
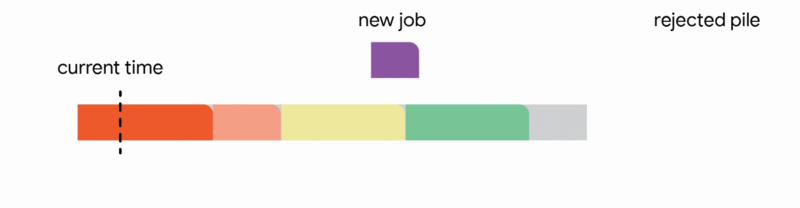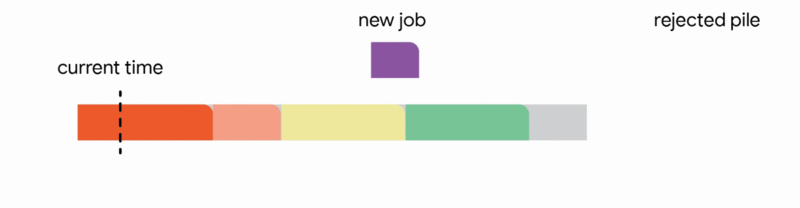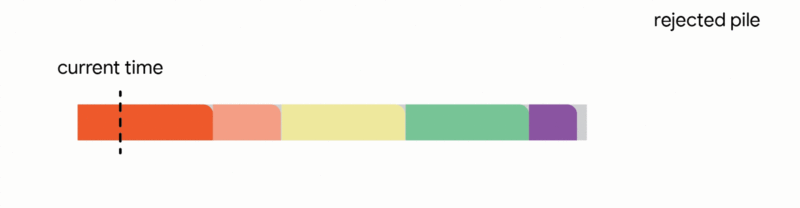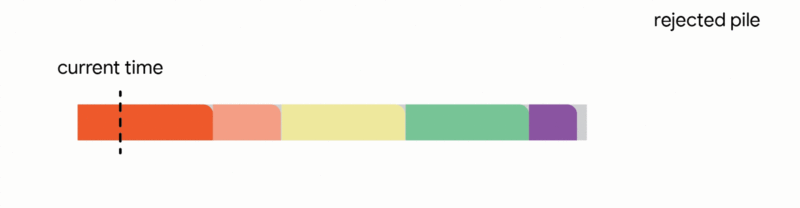
In this setting, our algorithm maintains a tentative schedule by assigning the jobs that have already arrived to disjoint time intervals. When a new job arrives, the algorithm modifies the tentative schedule by taking the first applicable action out of the following four actions:
1. Add the job to the tentative schedule by placing it in an empty interval
2. Replace another future job from the tentative schedule if the new job is significantly smaller
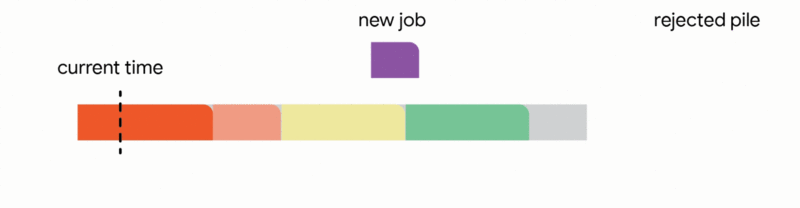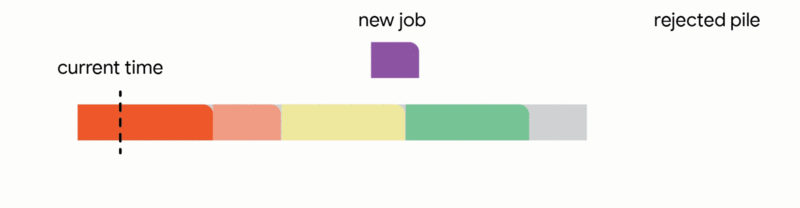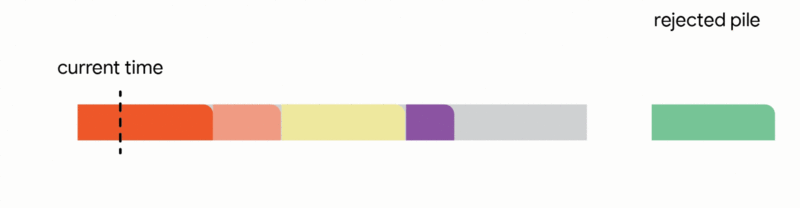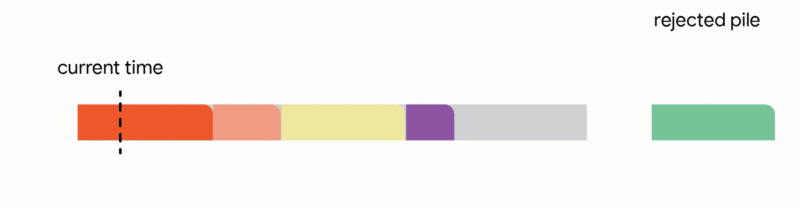
3. Interrupt the currently executing job if the new job is smaller than the remaining time of the executing job
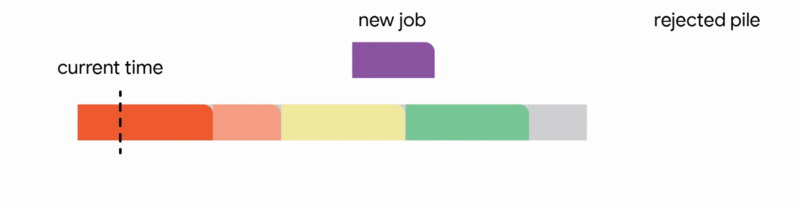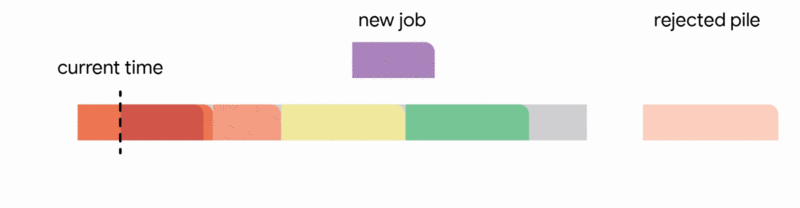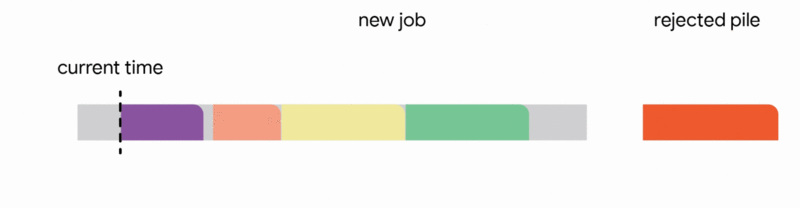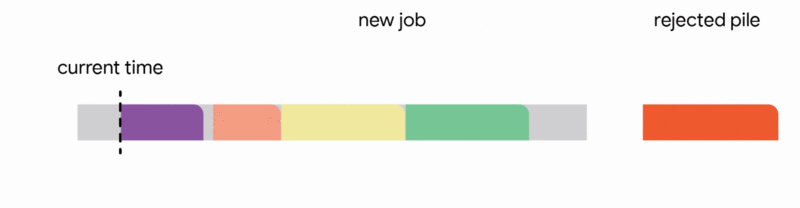
4. Discard the newly arrived job
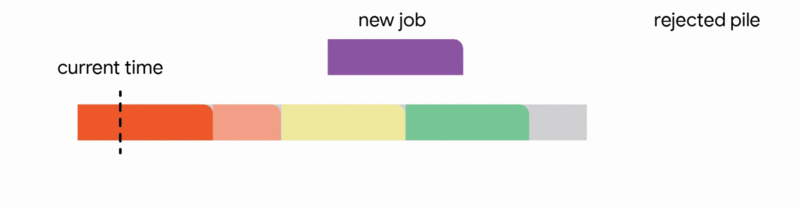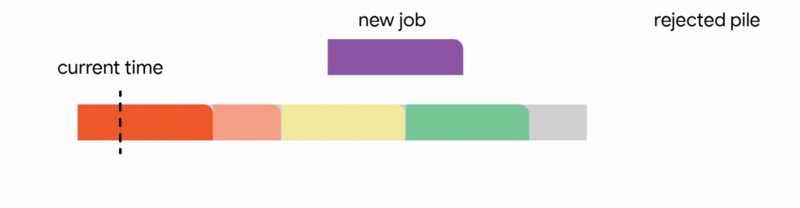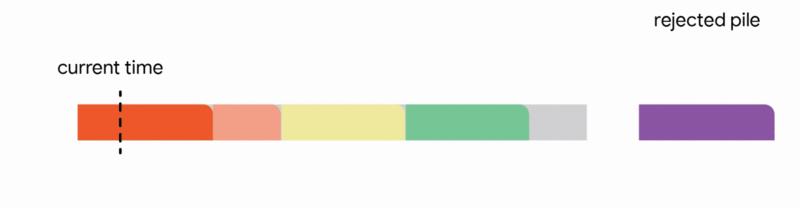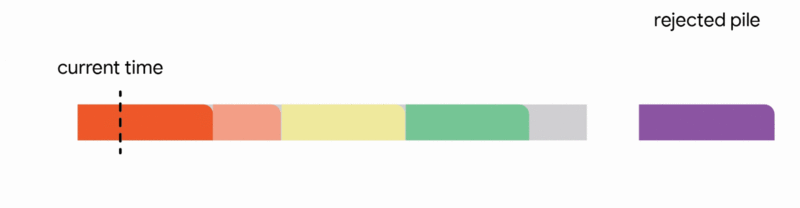
Our main result shows that a generalization of this algorithm to arbitrary capacity profiles gives the first constant competitive ratio for this problem. Formally, we obtain a competitive ratio of 1/11. While guaranteeing to schedule only ~9% of the optimal number of jobs sounds like a weak guarantee, this is a worst-case guarantee that holds even in the most adversarial situations.
Conclusion and future directions
As cloud infrastructure becomes more dynamic, the assumption of static capacity in scheduling algorithms no longer holds. This paper initiates the formal study of throughput maximization under time-varying capacity, bridging the gap between theoretical scheduling models and the fluctuating reality of data centers.
While we establish strong constant factor approximations, there is still room for growth. The gap between our 1/11 competitive ratio for the online setting and the theoretical upper bound of 1/2 suggests that more efficient algorithms may exist. Exploring randomized algorithms or scenarios with imperfect knowledge of future capacity could yield even better results for real-world applications.
Acknowledgments
This represents joint work with Aniket Murhekar (University of Illinois at Urbana Champaign), Zoya Svitkina (Google Research), Erik Vee (Google Research), and Joshua Wang (Google Research).
-
Labels:
- Algorithms & Theory