ML-fairness-gym: A Tool for Exploring Long-Term Impacts of Machine Learning Systems
February 5, 2020
Posted by Hansa Srinivasan, Software Engineer, Google Research
Quick links
Machine learning systems have been increasingly deployed to aid in high-impact decision-making, such as determining criminal sentencing, child welfare assessments, who receives medical attention and many other settings. Understanding whether such systems are fair is crucial, and requires an understanding of models’ short- and long-term effects. Common methods for assessing the fairness of machine learning systems involve evaluating disparities in error metrics on static datasets for various inputs to the system. Indeed, many existing ML fairness toolkits (e.g., AIF360, fairlearn, fairness-indicators, fairness-comparison) provide tools for performing such error-metric based analysis on existing datasets. While this sort of analysis may work for systems in simple environments, there are cases (e.g., systems with active data collection or significant feedback loops) where the context in which the algorithm operates is critical for understanding its impact. In these cases, the fairness of algorithmic decisions ideally would be analyzed with greater consideration for the environmental and temporal context than error metric-based techniques allow.
In order to facilitate algorithmic development with this broader context, we have released ML-fairness-gym, a set of components for building simple simulations that explore potential long-run impacts of deploying machine learning-based decision systems in social environments. In “Fairness is not Static: Deeper Understanding of Long Term Fairness via Simulation Studies” we demonstrate how the ML-fairness-gym can be used to research the long-term effects of automated decision systems on a number of established problems from current machine learning fairness literature.
An Example: The Lending Problem
A classic problem for considering fairness in machine learning systems is the lending problem, as described by Liu et al. This problem is a highly simplified and stylized representation of the lending process, where we focus on a single feedback loop in order to isolate its effects and study it in detail. In this problem formulation, the probability that individual applicants will pay back a loan is a function of their credit score. These applicants also belong to one of an arbitrary number of groups, with their group membership observable by the lending bank.
The groups start with different credit score distributions. The bank is trying to determine a threshold on the credit scores, applied across groups or tailored to each, that best enables the bank to reach its objectives. Applicants with scores higher than the threshold receive loans, and those with lower scores are rejected. When the simulation selects an individual, whether or not they will pay the loan is randomly determined based on their group’s probability of payback. In this example, individuals currently applying for loans may apply for additional loans in the future and thus, by paying back their loan, both their credit score and their group’s average credit score increases. Similarly, if the applicant defaults, the group’s average credit score decreases.
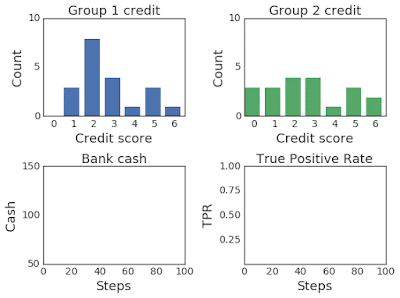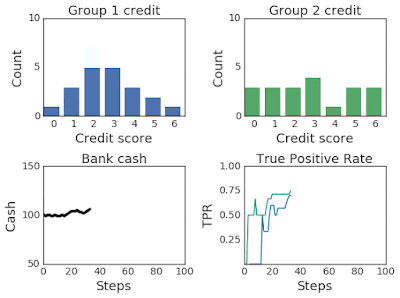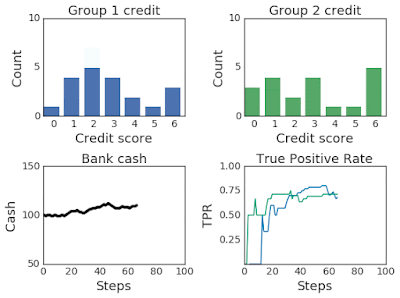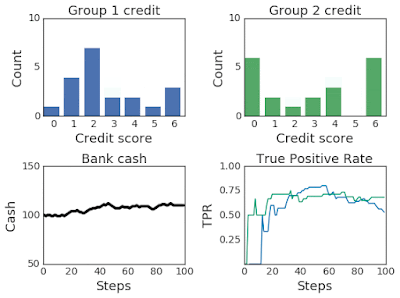
The most effective threshold settings will depend on the bank’s goals. A profit-maximizing bank may set a threshold that maximizes the predicted return, based on the estimated likelihood that applicants will repay their loans. Another bank, seeking to be fair to both groups, may try to implement thresholds that maximize profit while satisfying equality of opportunity, the goal of which is to have equal true positive rates (TPR is also called recall or sensitivity; a measure of what fraction of applicants who would have paid back loans were given a loan). In this scenario, machine learning techniques are employed by the bank to determine the most effective threshold based on loans that have been distributed and their outcomes. However, since these techniques are often focused on short-term objectives, they may have unintended and unfair consequences for different groups.
A standard practice in machine learning to assess the impact of a scenario like the lending problem is to reserve a portion of the data as a “test set”, and use that to calculate relevant performance metrics. Fairness is then assessed by looking at how those performance metrics differ across salient groups. However, it is well understood that there are two main issues with using test sets like this in systems with feedback. If test sets are generated from existing systems, they may be incomplete or reflect the biases inherent to those systems. In the lending example, a test set could be incomplete because it may only have information on whether an applicant who has been given a loan has defaulted or repaid. Consequently, the dataset may not include individuals for whom loans have not been approved or who have not had access to loans before.
The second issue is that actions informed by the output of the ML system can have effects that may influence their future input. The thresholds determined by the ML system are used to extend loans. Whether people default or repay these loans then affects their future credit score, which then feed back into the ML system.
These issues highlight the shortcomings of assessing fairness in static datasets and motivate the need for analyzing the fairness of algorithms in the context of the dynamic systems in which they are deployed. We created the ML-fairness-gym framework to help ML practitioners bring simulation-based analysis to their ML systems, an approach that has proven effective in many fields for analyzing dynamic systems where closed form analysis is difficult.
ML-fairness-gym as a Simulation Tool for Long-Term Analysis
The ML-fairness-gym simulates sequential decision making using Open AI’s Gym framework. In this framework, agents interact with simulated environments in a loop. At each step, an agent chooses an action that then affects the environment’s state. The environment then reveals an observation that the agent uses to inform its subsequent actions. In this framework, environments model the system and dynamics of the problem and observations serve as data to the agent, which can be encoded as a machine learning system.
Fairness Is Not Static: Extending the Analysis to the Long-Term
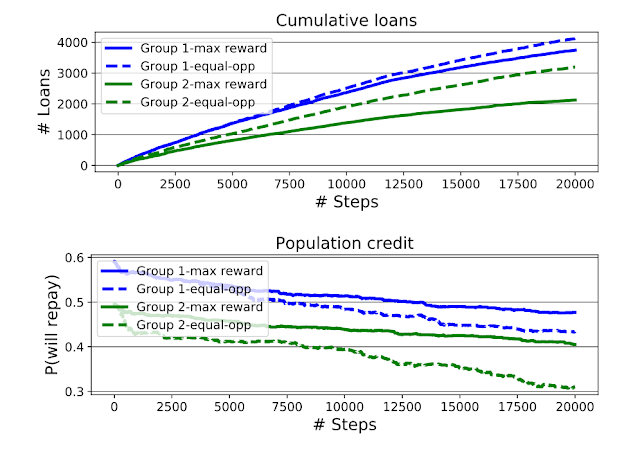
Since Liu et al.’s original formulation of the lending problem examined only the short-term consequences of the bank’s policies — including short-term profit-maximizing policies (called the max reward agent) and policies subject to an equality of opportunity (EO) constraint — we use the ML-fairness-gym to extend the analysis to the long-term (many steps) via simulation.
The second finding is that equal opportunity constraints — enforcing equalized TPR between groups at each step — does not equalize TPR in aggregate over the simulation. This perhaps counterintuitive result can be thought of as an instance of Simpson’s paradox. As seen in the chart below, equal TPR in each of two years does not imply equal TPR in aggregate. This demonstrates how the equality of opportunity metric is difficult to interpret when the underlying population is evolving, and suggests that more careful analysis is necessary to ensure that the ML system is having the desired effects.
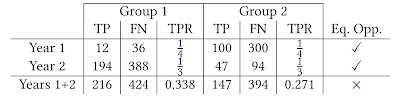 |
| An example of Simpson's paradox. TP are the true positive classifications, FN corresponds to the false negative classifications and TPR is the true positive rate. In years 1 and 2, the lender applies a policy that achieves equal TPR between the two groups. The aggregation over both years does not have equal TPR. |
While we focused on our findings for the lending problem in this blog post, the ML-fairness-gym can be used to tackle a wide variety of fairness problems. Our paper extends the analysis of two other scenarios that have been previously studied in the academic ML fairness literature. The ML-fairness-gym framework is also flexible enough to simulate and explore problems where “fairness” is under-explored. For example, in a supporting paper, “Fair treatment allocations in social networks,” we explore a stylized version of epidemic control, which we call the precision disease control problem, to better understand notions of fairness across individuals and communities in a social network.
We’re excited about the potential of the ML-fairness-gym to help other researchers and machine learning developers better understand the effects that machine learning algorithms have on our society, and to inform the development of more responsible and fair machine learning systems. Find the code and papers in the ML-fairness-gym Github repository.
-
Labels:
- Machine Intelligence
- Responsible AI
Quick links
×
❮
❯