Mechanism design for large language models
February 13, 2025
Paul Duetting and Song Zuo, Research Scientists
We investigate the design of auction mechanisms for aggregating the output of multiple self-interested LLMs into one joint output. We argue that this comes with a number of unique challenges, and we propose a simple token auction mechanism and illustrate our design through demonstration with an off-the-shelf LLM.
Quick links
Generative AI and large language models (LLMs) facilitate the automated generation of assets across a variety of domains. For many use cases, several LLM agents may need to collaborate to create a joint output. A potential example is in the context of Internet ads, where advertisers might be represented by LLM agents capable of producing ads in reply to a user query. Or it could be that the LLMs represent stakeholders of a company, working together to write a joint report.
Consider an example situation where there is a single space on a webpage to be filled with an ad creative in reply to a user searching for “Vacations in Hawaii”. Suppose there are two advertisers interested in this search query, Alpha Airlines and Beta Resort, each represented by an LLM agent. Each LLM agent is capable of producing an ad creative in reply to the search query. For example: “Fly to Hawaii with Alpha Airlines” and “Enjoy the beauty of Hawaii at Beta Resort”. However, in this case, a suitable auction design would be flexible enough to enable the creation of a joint ad creative, such as “Alpha Airlines flies you to Hawaii where you can enjoy a magic weeklong experience at Beta Resort”.
An illustrative example, consider separate LLM agents representing two hypothetical advertisers, Alpha Airlines and Beta Resort, which are tasked to collaborate to produce a joint ad creative.
In applications like this, each LLM agent has (potentially diverging) preferences for the joint output. For example, advertisers prefer to have their products or services mentioned, while also caring about different aspects that they wish to mention more prominently. Problems in which multiple agents collaborate to select a joint output naturally call for a mechanism design (i.e., auction design) approach.
In “Mechanism Design for Large Language Models”, which won the WWW 2024 Best Paper Award, we argue that the problem of joint output generation through multiple LLM agents comes with several unique challenges, and we present a new class of auction mechanisms tailored to address the key challenges of this novel application domain. We describe theoretical results that inform the design of auctions
The token auction model
At a high-level, our approach — which we dub the token auction model — mimics the mechanics of LLMs as closely as possible. The token auction operates on a token-by-token basis and functions like one giant LLM, while also defining some payment function, monetary or otherwise. We illustrate the key ideas and concepts in the context of text creation, but the same ideas apply to the creation of other media types (such as images or videos). In this context, a token is simply an individual word, a sequence of words, punctuation mark, etc. There is also a special “end” token signifying the end of the creation process.
Let’s first look at how an individual LLM works. On an abstract level, an LLM defines for any sequence of input tokens, a distribution over tokens. For example, the input sequence could be “Mechanism Design for”, and the output distribution could be [(“Large”, 0.8), (“Generative”, 0.2)], meaning that the next token should be “Large” with 80% probability and “Generative” with 20%. This functionality can then be used for so-called auto-regressive text generation. The process starts with an initial prompt, which is just a sequence of tokens. Then a token is sampled from the distribution over tokens defined by the LLM. This token is appended to the sequence being generated. Then the process is repeated with the resulting expanded sequence of tokens until the special “end” token is sampled.
The token auction performs two key tasks: it expands the shared token sequence and determines agent payments. Both of these tasks are achieved through functions, which we refer to as the distribution aggregation function and the payment function. Both functions take as input the distributions of the individual LLMs and a bid by each agent. The distribution aggregation function maps this to a distribution over tokens, while the output of the payment function is a vector of payments.
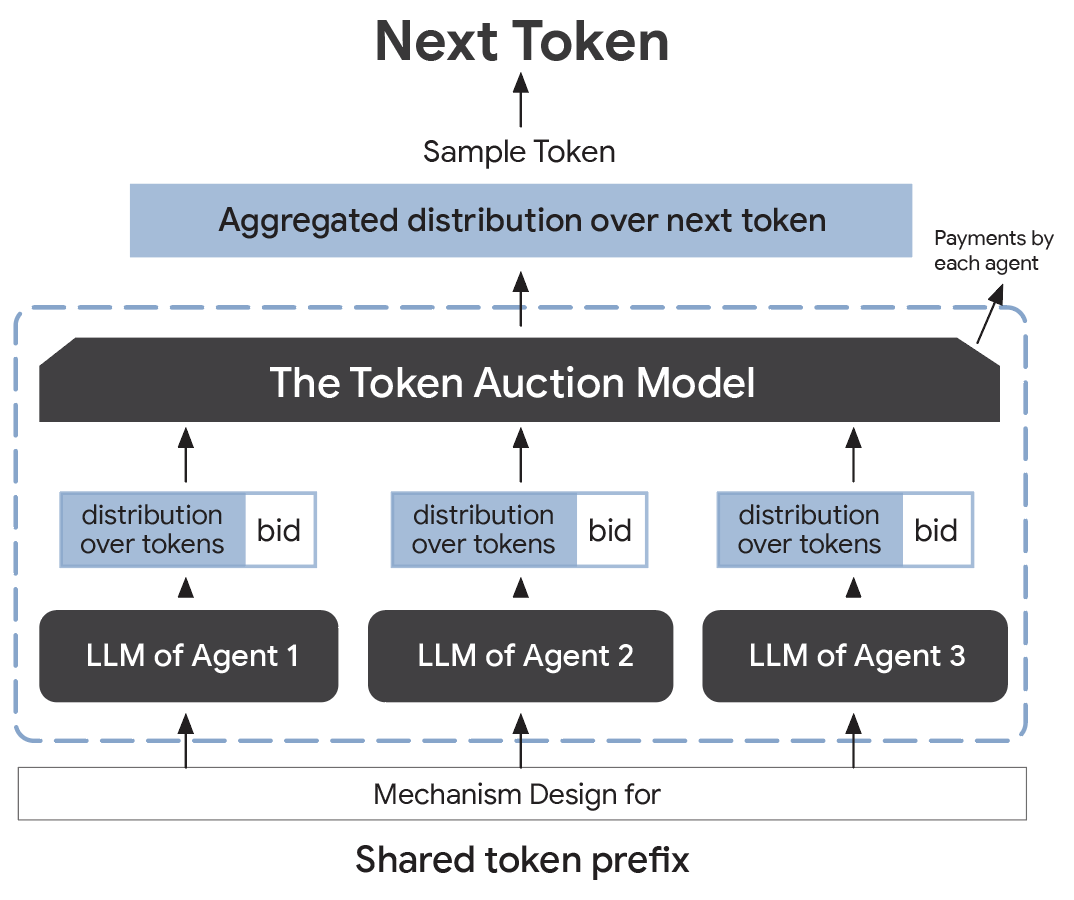
The token auction model architecture.
For example, in the situation illustrated in the figure above, the shared sequence of tokens might be “Mechanism Design for”. The distributions might be [(“Large”, 0.8), (“Generative”, 0.2)] for the LLM of Agent 1, (“Large”, 1.0) for the LLM of Agent 2, and (“Generative”, 1.0) for the LLM of Agent 3. The bids might be 1, 2, and 2, respectively. A possible aggregated distribution would be the bid-weighted average of the distributions, namely [(“Large”, 0.56), (“Generative”, 0.44)]. A possible choice for the payments would be to ask each agent to pay their bid, which would have the agents commit 1, 2, and 2, respectively.
For our theoretical analysis of this model (and possible choices of distribution aggregation functions and payment functions), we assume that the agents truthfully report their distributions, but may be strategic about their bids. We believe this is a realistic assumption, as LLMs encode preferences over output text in a succinct and non-obvious way. Moreover, in order for the token auction to be able to aggregate distributions, we need to have (at least) some (minimal) information about agent’s preferences away from their “preferred” distributions. Our approach here is to assume that the agents have (known) partial preference orders over distributions. That is, we assume that agents may be able to rank some, but not all, pairs of distributions.
Main technical results
We present a suite of theoretical results for the token auction model, focusing on a single step in the generation process.
Design space reduction
The first result is a “design space reduction”, which confines the general space of distribution aggregation functions to a much smaller sub-space. Inspired by successful practical auction designs, we formulate two desirable properties that a token-auction mechanism should satisfy, namely “payment monotonicity” and “consistent aggregation”, and show that these are equivalent to requiring monotonicity of the distribution aggregation function. Thus, we can restrict attention to monotone distribution aggregation functions, meaning that if an agent weakly increases their bid, the aggregated distribution function would only change to a distribution weakly preferred by the agent (see paper for details).
“Second-price” payments
Next, we explore the design of payment rules. An important insight of auction theory is that second-price payments provide good incentives. In the context of a single-item auction, the idea is to give the item to the bidder with the highest bid, but make that bidder only pay the second-highest bid. As our second result, we show that (under some additional, natural assumptions) any monotone distribution aggregation function admits an analog of such second-price payments. For this we show that any such rule admits a stable sampling, i.e., an implementation of the distribution aggregation function based on an explicit random seed that, for each seed, outputs only one of two tokens depending on whether the bid is below or above a certain threshold.
Optimal aggregation rules
As our final set of results, we explore the design of optimal distribution aggregation functions. Taking inspiration from state-of-the-art LLM training, we formulate aggregated loss functions that associate with each output distribution a total loss that we seek to minimize. We consider two different formulations of the aggregated loss functions, and show that these correspond to two simple distribution aggregation functions. The first is a linear distribution aggregation function, which outputs the bid-weighted average of the distributions. The second is a log-linear distribution aggregation function, which does the same in log space.
Demonstration
We also conducted a series of experiments with our proposed design. For the demonstrations we used prompt tuning on an off-the-shelf LLM. That is, rather than taking a specifically trained model, we instructed the LLM with a prompt to act on behalf of a hypothetical advertiser.
In the example discussed here, there are two advertisers, “Alpha Airlines” and “Beta Resort”, which want to advertise a flight with the airline and a stay at the hotel, respectively. (See the paper for the prompts that we used). Below we show the output of the token auction (parameterized by λ, the relative weight of the bid of Alpha Airlines). The first column shows the output for the linear aggregation rule, and the second column shows the output for the log-linear aggregation rule. In both cases, the behavior is as intended with ad creatives shifting from mentioning only Alpha Airlines, to mentioning both Alpha Airlines and Beta Resort, to only mentioning Beta Resort.
Additional demonstrations with different prompts, including settings with competing advertisers can be found in the paper.
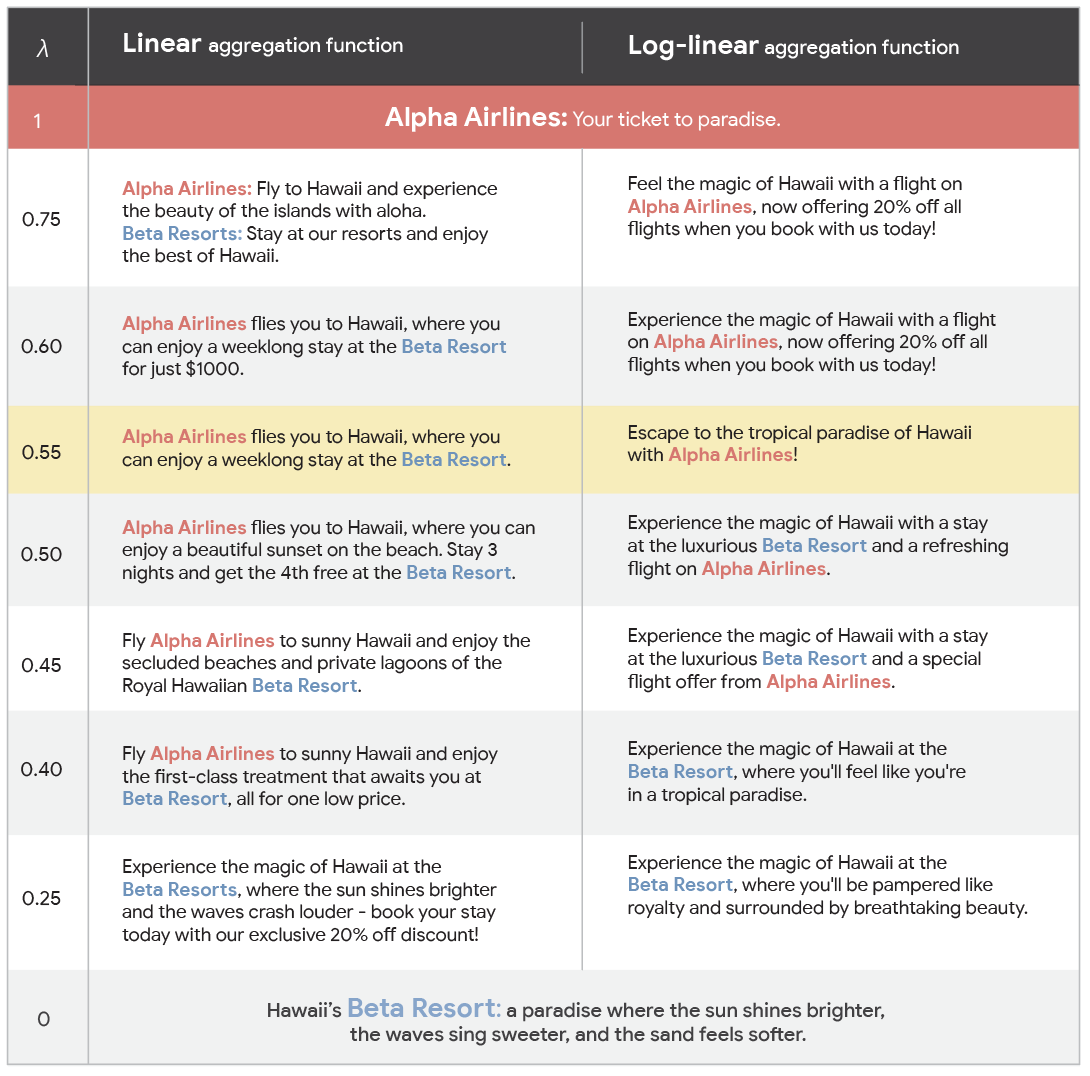
Output generated by the two distribution aggregation functions, as a function of the relative weight of the bid by Alpha Airlines.
Conclusion
In this research, we designed a mechanism for aggregating LLM output. Our proposed format allows the LLM agents to influence the output through single-dimensional bids. The mechanism’s design makes minimal assumptions about the agents’ preferences. Working under this paradigm, we showed that the natural requirements on the auction mechanism’s incentive properties called for monotone aggregation. We then showed that under robust preferences, any monotone aggregation function enables second-price–style payments. As a “proof of concept” for our designed mechanism, we demonstrated promising outcomes of our aggregation methods by implementing these aggregation functions in a real-world state-of-the-art LLM using prompt tuning.
Acknowledgements
The work described in this blog post is joint work with Vahab Mirroni, Renato Paes Leme, and Haifeng Xu. We thank Dirk Bergemann, Marina Halac, Philipp Strack, Elliot Lipnowski, Yang Cai, Vasilis Syrgkanis, Negin Gorezaei, Ido Cohen, Yoav Nagel, Yael Shemesh as well as the participants of the Yale Economics Seminar, the Stanford MS&E Seminar, the WWW 2024 conference, and the INFORMS Revenue and Management Pricing Section Conference for invaluable comments and suggestions to improve this manuscript. We are especially grateful to Yong Cheng from Google DeepMind for his expert guidance on the LLM-related details and literature.




