Making quantum error correction work
December 9, 2024
Michael Newman and Kevin Satzinger, Research Scientists, Google Research, Google Quantum AI team
Today we introduce Willow, the first quantum processor where error-corrected qubits get exponentially better as they get bigger.
Quick links
Quantum computers offer promising applications in many fields, ranging from chemistry and drug discovery to optimization and cryptography. Most of these applications require billions if not trillions of operations to execute reliably — not much compared to what your web browser is doing right now. But quantum information is delicate, and even state-of-the-art quantum devices will typically experience at least one failure in every thousand operations. To achieve their potential, performance needs to improve dramatically.
Today in “Quantum error correction below the surface code threshold,” published in Nature, we report a qualitative change in the way quantum computers perform. This change is powered by combining quantum error correction with our latest superconducting quantum processor, Willow. Willow is the first processor where error-corrected qubits get exponentially better as they get bigger. Each time we increase our encoded qubits from a 3x3 to a 5x5 to a 7x7 lattice of physical qubits, the encoded error rate is suppressed by a factor of two. This demonstrates the exponential error suppression promised by quantum error correction, a nearly 30-year-old goal for quantum computing and the key element to unlocking large-scale quantum applications.
Error-corrected qubits that get better as they get bigger
To make quantum computers more reliable, we can group qubits to work together to correct errors. In surface code quantum computing, each group consists of a dxd square lattice of qubits called a surface code, and each surface code represents a single encoded or “logical” qubit. The bigger a surface code lattice, the more errors it can tolerate. The expectation is that as the lattice gets bigger, the logical qubit is more and more protected, and the logical performance improves.
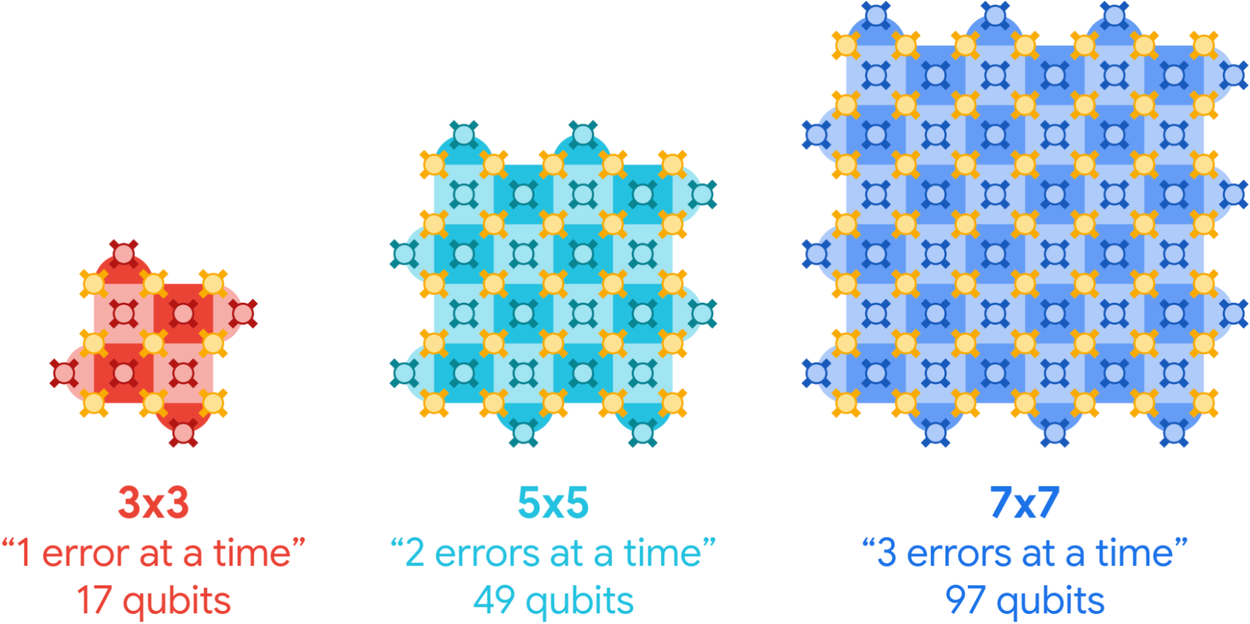
Surface code logical qubits of increasing sizes, each able to correct more errors than the last. The encoded quantum state is stored on the array of data qubits (gold). Measure qubits (red, cyan, blue) check for errors on the neighboring data qubits.
But there’s a subtlety: making the lattice bigger also introduces more opportunities for error. If the error rate of the physical qubits is too high, these extra errors overwhelm the error correction so that making the lattice bigger just makes the processor’s performance worse. Conversely, if the error rate of the physical qubits is sufficiently low, then error correction more than makes up for these extra errors. In fact, the encoded error rate goes down exponentially as more qubits are added.
The critical error rate that divides these two cases, below which quantum error correction transforms from harmful to helpful, is called the threshold.
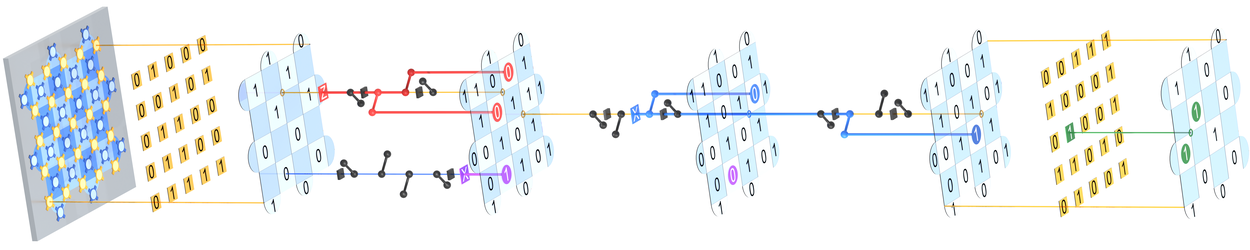
A day in the life of a logical qubit. Time progresses left to right. We initialize the data qubits (gold) in a known state and make repeated parity checks that can highlight errors (red, purple, blue, green). At the end, we measure the data qubits and decode the measurement data to arrive at an error-corrected logical measurement.
Willow: beating the threshold
Operating “below the threshold” has been a goal for error corrected quantum computing since its inception in the 1990s. However, after almost 30 years of advancement in device fabrication, calibration, and qubit design, quantum computers still hadn’t passed this landmark. That is, until our latest 105-qubit superconducting processor, Willow.
Willow represents a significant leap forward in quantum hardware. It maintains the tunability of our previous architecture, Sycamore, while improving the average qubit lifetimes (T1) from about 20 μs to 68 µs ± 13 µs. The qubits and operations in our device are optimized with quantum error correction in mind, and run alongside our error correction software, including state-of-the-art machine learning, reinforcement learning, and graph-based algorithms to identify and correct errors accurately.
Using Willow, we report the first ever demonstration of exponential error suppression with increasing surface code size. Each time we increase our lattice in size from 3x3 to 5x5 to 7x7, the encoded error rate decreases by a factor of 2.14. This culminates in a logical qubit whose lifetime is more than twice that of its best constituent physical qubit, demonstrating the capacity of an error-corrected qubit to go beyond its physical components.
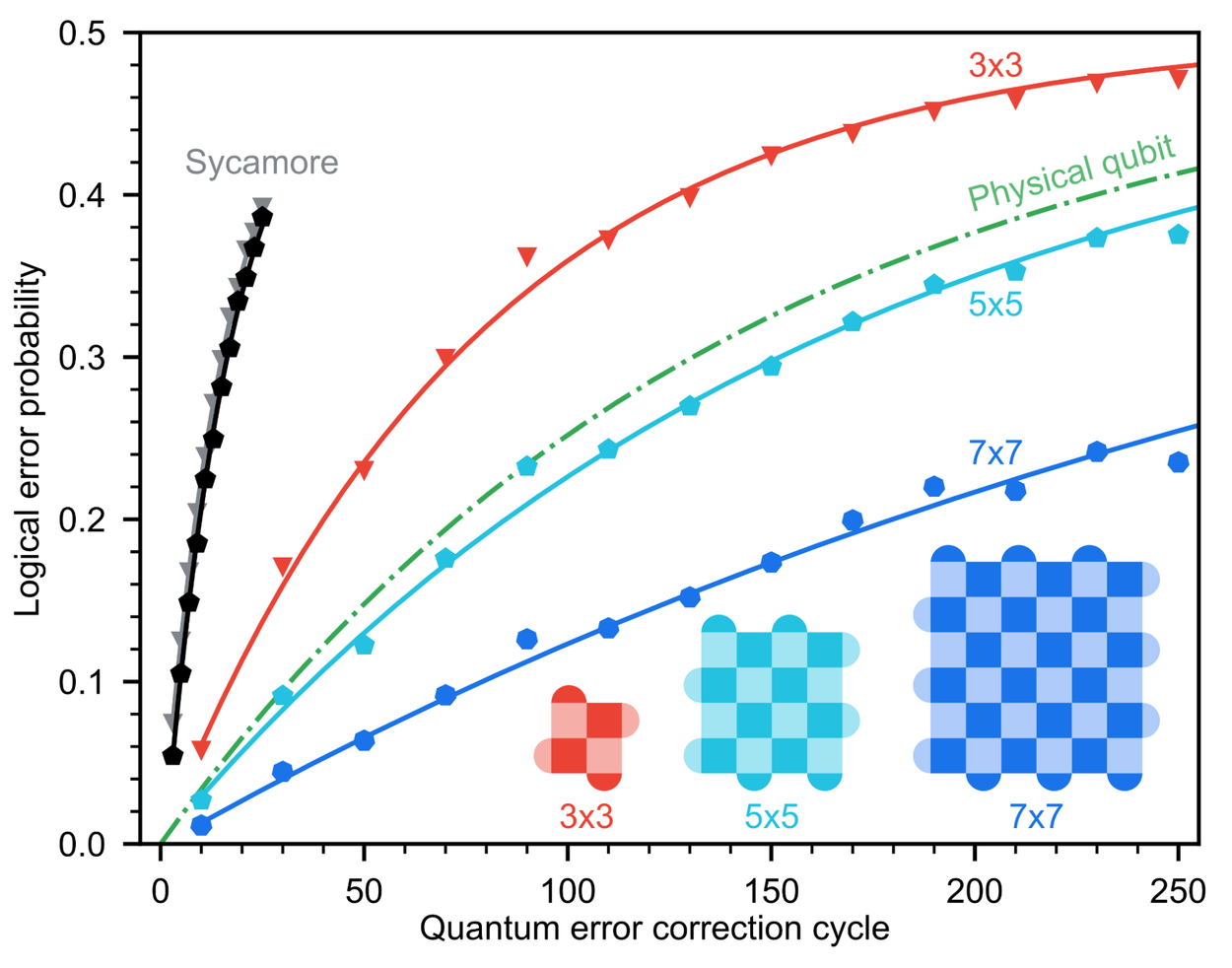
Logical qubit performance scaling with surface code size. As we grow from 3x3 (red) to 5x5 (cyan) to 7x7 (blue), the logical error probability drops substantially. The 7x7 logical qubit on Willow lives twice as long as its best physical qubit (green) and twenty times longer than our previous surface code in Sycamore (gray, black).
Looking to the future
Once you pass the threshold, small improvements in the device are amplified exponentially with quantum error correction. For example, while the operation fidelities in Willow are about twice as good as Sycamore, the encoded error rates are about twenty times better. Anticipating this rapid improvement, we can look ahead to questions that will be relevant to future error-corrected quantum computers.
Can we build a near-perfect encoded qubit?
Quantum error correction looks like it’s working now, but there’s a big gap between the one-in-a-thousand error rates of today and the one-in-a-trillion error rates needed tomorrow. Could we run into new physics that could prevent us from building a quantum computer?
To answer this, we build repetition codes. Unlike surface codes, which protect against all (local) quantum errors, repetition codes focus solely on bitflip errors, but do so far more efficiently. By running experiments with repetition codes and ignoring other error types, we achieve lower encoded error rates while employing many of the same error correction principles as the surface code. The repetition code acts as an advance scout for checking whether error correction will work all the way down to the near-perfect encoded error rates we’ll ultimately need.
When running repetition codes on Willow, we are able to realize nearly 10 billion cycles of error correction without seeing an error. Exhibiting that level of control over a quantum system, even when only protecting against bitflip errors, is quite exciting. But there’s a catch — when we try to push the encoded error rate lower by increasing the size of the code further, it won’t budge. The reason for this behavior is currently under investigation, and we’re confident that we can find it and fix it, just as we fixed a similar problem with high-energy radiation on Sycamore.
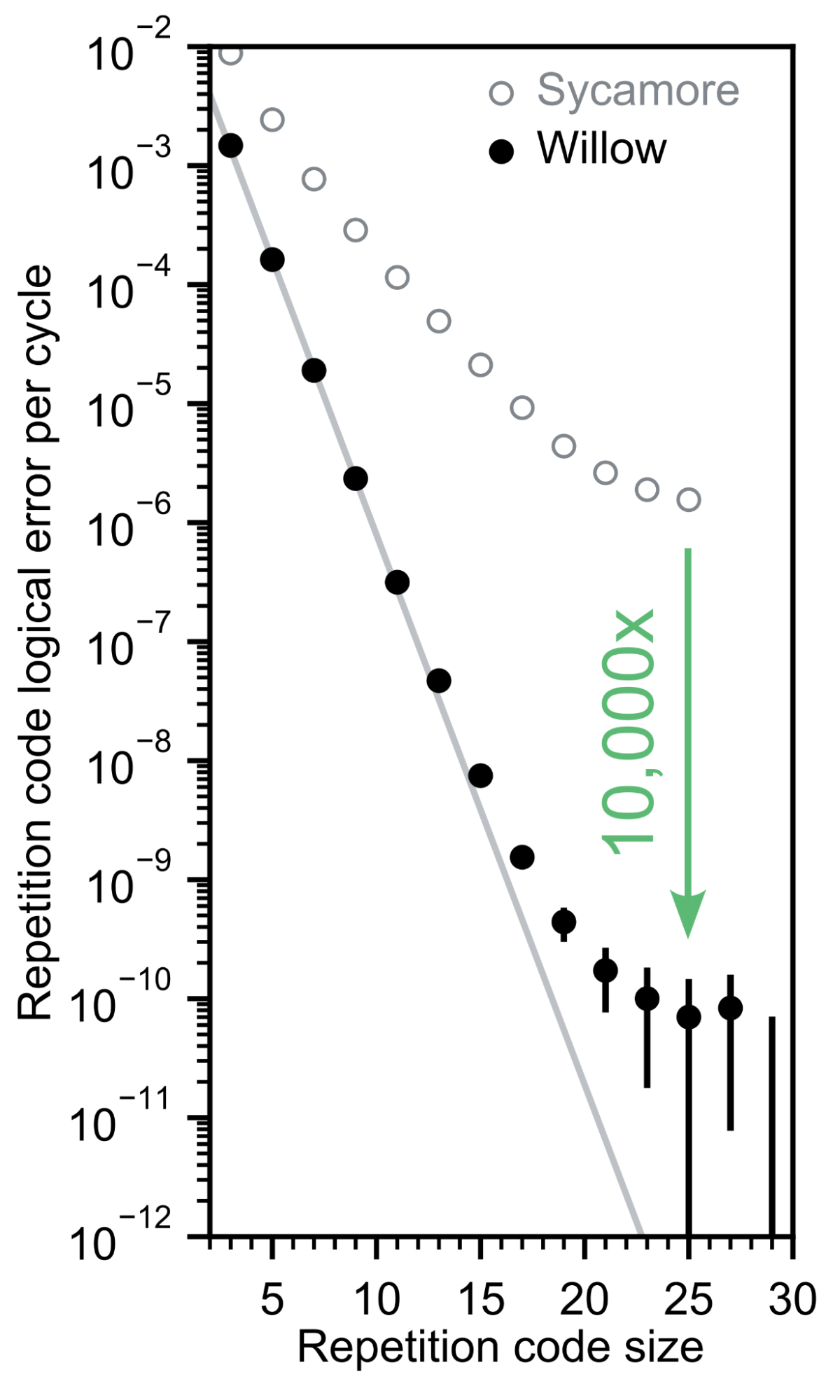
Repetition code performance scaling with repetition code size. We achieve a 10,000x improvement compared to Sycamore, but observe an error floor around 10-10 logical error per cycle.
Can we make error-corrected quantum computers fast?
Compared to the gigahertz-frequency device you’re probably reading this blog on, error-corrected quantum computers are actually quite slow. Even superconducting quantum computers, which are one of the fastest qubit technologies, have measurement times that are about a microsecond long. The sub-nanosecond timescales of classical operations are more than a thousand times faster.
Quantum error-corrected operations can be even slower, in part because we must also interpret measurements to identify errors. This is done by classical software called a quantum error decoder, which must process measurement information at the rate the quantum computer produces it.
In a first for superconducting qubits, we demonstrate the ability to decode measurement information in real time alongside the device. This is great news, but it must also be tempered. Even when decoding is keeping up with the device, for certain error-corrected operations, the decoder can still slow things down. We measure a decoder delay time of 50 to 100 microseconds on our device, and anticipate it will increase at larger lattice sizes. This delay could significantly impact the speed of error-corrected operation, and if quantum computers are to become practical tools for scientific discovery, we need to improve upon it.
What’s next?
With error correction, we can now in principle scale up our system to realize near-perfect quantum computing. In practice, it’s not so easy — we still have a long way to go before we reach our goal of building a large-scale, fault-tolerant quantum computer.
Logical qubits on progressively better processors, with a 2x improvement in physical qubits and increasing size each step up. Red and blue squares correspond to parity checks indicating nearby errors. The processors can reliably execute roughly 50, 103, 106, and 1012 cycles, respectively.
At current physical error rates, we might need more than a thousand physical qubits per surface code grid to realize relatively modest encoded error rates of 10-6. Furthermore, all of this was accomplished on a 105-qubit processor; can we achieve the same performance on a 1,000-qubit processor? What about a million-qubit processor? The engineering challenge ahead of us is immense.
At the same time, progress has been staggering, and the improvement offered by quantum error correction is exponential. We have seen a 20x increase in encoded performance since last year — how many more 20x steps until we can run large-scale quantum algorithms? Maybe fewer than you think.
To foster collaboration and accelerate progress, we invite researchers, engineers, and developers to join us on this journey by checking out our open source software and educational resources, including a new free Coursera course dedicated to quantum error correction.






