How Can Neural Network Similarity Help Us Understand Training and Generalization?

In order to solve tasks, deep neural networks (DNNs) progressively transform input data into a sequence of complex representations (i.e., patterns of activations across individual neurons). Understanding these representations is critically important, not only for interpretability, but also so that we can more intelligently design machine learning systems. However, understanding these representations has proven quite difficult, especially when comparing representations across networks. In a previous post, we outlined the benefits of Canonical Correlation Analysis (CCA) as a tool for understanding and comparing the representations of convolutional neural networks (CNNs), showing that they converge in a bottom-up pattern, with early layers converging to their final representations before later layers over the course of training.

In “Insights on Representational Similarity in Neural Networks with Canonical Correlation” we develop this work further to provide new insights into the representational similarity of CNNs, including differences between networks which memorize (e.g., networks which can only classify images they have seen before) from those which generalize (e.g., networks which can correctly classify previously unseen images). Importantly, we also extend this method to provide insights into the dynamics of recurrent neural networks (RNNs), a class of models that are particularly useful for sequential data, such as language. Comparing RNNs is difficult in many of the same ways as CNNs, but RNNs present the additional challenge that their representations change over the course of a sequence. This makes CCA, with its helpful invariances, an ideal tool for studying RNNs in addition to CNNs. As such, we have additionally open sourced the code used for applying CCA on neural networks with the hope that will help the research community better understand network dynamics.

Representational Similarity of Memorizing and Generalizing CNNs
Ultimately, a machine learning system is only useful if it can generalize to new situations it has never seen before. Understanding the factors which differentiate between networks that generalize and those that don’t is therefore essential, and may lead to new methods to improve generalization performance. To investigate whether representational similarity is predictive of generalization, we studied two types of CNNs:

• generalizing networks: CNNs trained on data with unmodified, accurate labels and which learn solutions which generalize to novel data.
• memorizing networks: CNNs trained on datasets with randomized labels such that they must memorize the training data and cannot, by definition, generalize (as in Zhang et al., 2017).

We trained multiple instances of each network, differing only in the initial randomized values of the network weights and the order of the training data, and used a new weighted approach to calculate the CCA distance measure (see our paper for details) to compare the representations within each group of networks and between memorizing and generalizing networks.

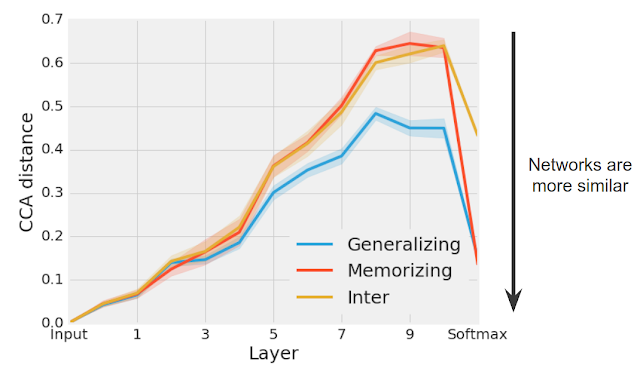
We found that groups of different generalizing networks consistently converged to more similar representations (especially in later layers) than groups of memorizing networks (see figure below). At the softmax, which denotes the network’s ultimate prediction, the CCA distance for each group of generalizing and memorizing networks decreases substantially, as the networks in each separate group make similar predictions.

Groups of generalizing networks (blue) converge to more similar solutions than groups of memorizing networks (red). CCA distance was calculated between groups of networks trained on real CIFAR-10 labels (“Generalizing”) or randomized CIFAR-10 labels (“Memorizing”) and between pairs of memorizing and generalizing networks (“Inter”).

Perhaps most surprisingly, in later hidden layers, the representational distance between any given pair of memorizing networks was about the same as the representational distance between a memorizing and generalizing network (“Inter” in the plot above), despite the fact that these networks were trained on data with entirely different labels. Intuitively, this result suggests that while there are many different ways to memorize the training data (resulting in greater CCA distances), there are fewer ways to learn generalizable solutions. In future work, we plan to explore whether this insight can be used to regularize networks to learn more generalizable solutions.

Understanding the Training Dynamics of Recurrent Neural Networks
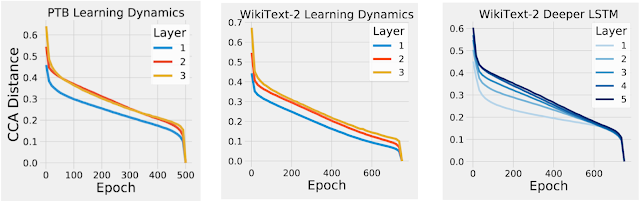
So far, we have only applied CCA to CNNs trained on image data. However, CCA can also be applied to calculate representational similarity in RNNs, both over the course of training and over the course of a sequence. Applying CCA to RNNs, we first asked whether the RNNs exhibit the same bottom-up convergence pattern we observed in our previous work for CNNs. To test this, we measured the CCA distance between the representation at each layer of the RNN over the course of training with its final representation at the end of training. We found that the CCA distance for layers closer to the input dropped earlier in training than for deeper layers, demonstrating that, like CNNs, RNNs also converge in a bottom-up pattern (see figure below).

Convergence dynamics for RNNs over the course of training exhibit bottom up convergence, as layers closer to the input converge to their final representations earlier in training than later layers. For example, layer 1 converges to its final representation earlier in training than layer 2 than layer 3 and so on. Epoch designates the number of times the model has seen the entire training set while different colors represent the convergence dynamics of different layers.

Additional findings in our paper show that wider networks (e.g., networks with more neurons at each layer) converge to more similar solutions than narrow networks. We also found that trained networks with identical structures but different learning rates converge to distinct clusters with similar performance, but highly dissimilar representations. We also apply CCA to RNN dynamics over the course of a single sequence, rather than simply over the course of training, providing some initial insights into the various factors which influence RNN representations over time.

Conclusions
These findings reinforce the utility of analyzing and comparing DNN representations in order to provide insights into network function, generalization, and convergence. However, there are still many open questions: in future work, we hope to uncover which aspects of the representation are conserved across networks, both in CNNs and RNNs, and whether these insights can be used to improve network performance. We encourage others to try out the code used for the paper to investigate what CCA can tell us about other neural networks!

Acknowledgements
Special thanks to Samy Bengio, who is a co-author on this work. We also thank Martin Wattenberg, Jascha Sohl-Dickstein and Jon Kleinberg for helpful comments.