Dynamic surface codes open new avenues for quantum error correction
January 13, 2026
Alec Eickbusch and Alexis Morvan, Research Scientists, Google Research, Google Quantum AI team
We present results showing the operation of new dynamic circuits for quantum error correction, going beyond their static counterparts by using fewer couplers, removing correlated errors, and utilizing a different type of quantum gate.
Quick links
Quantum error correction (QEC) is crucial for reaching the ultra low error rate necessary for useful quantum algorithms. At Google Quantum AI, our quantum processors use physical qubits constructed from small superconducting circuits, which are susceptible to noise. QEC allows us to combine numerous physical qubits into logical qubits, which are robust to noise.
In December 2024, we announced that operation of error correction on our Willow quantum processor was below threshold, signifying that the logical qubit's robustness to errors exponentially increases as more physical qubits are added. This demonstration utilized a surface code for high-performance quantum error-correction. During the operation of this surface code, we employed a static circuit, i.e., a single consistent set of underlying physical operations was executed repeatedly to measure and correct errors. These static circuits, while useful for realizing QEC on a device with full yield, limit the ability to avoid "dropouts" — qubits or couplers that fail.
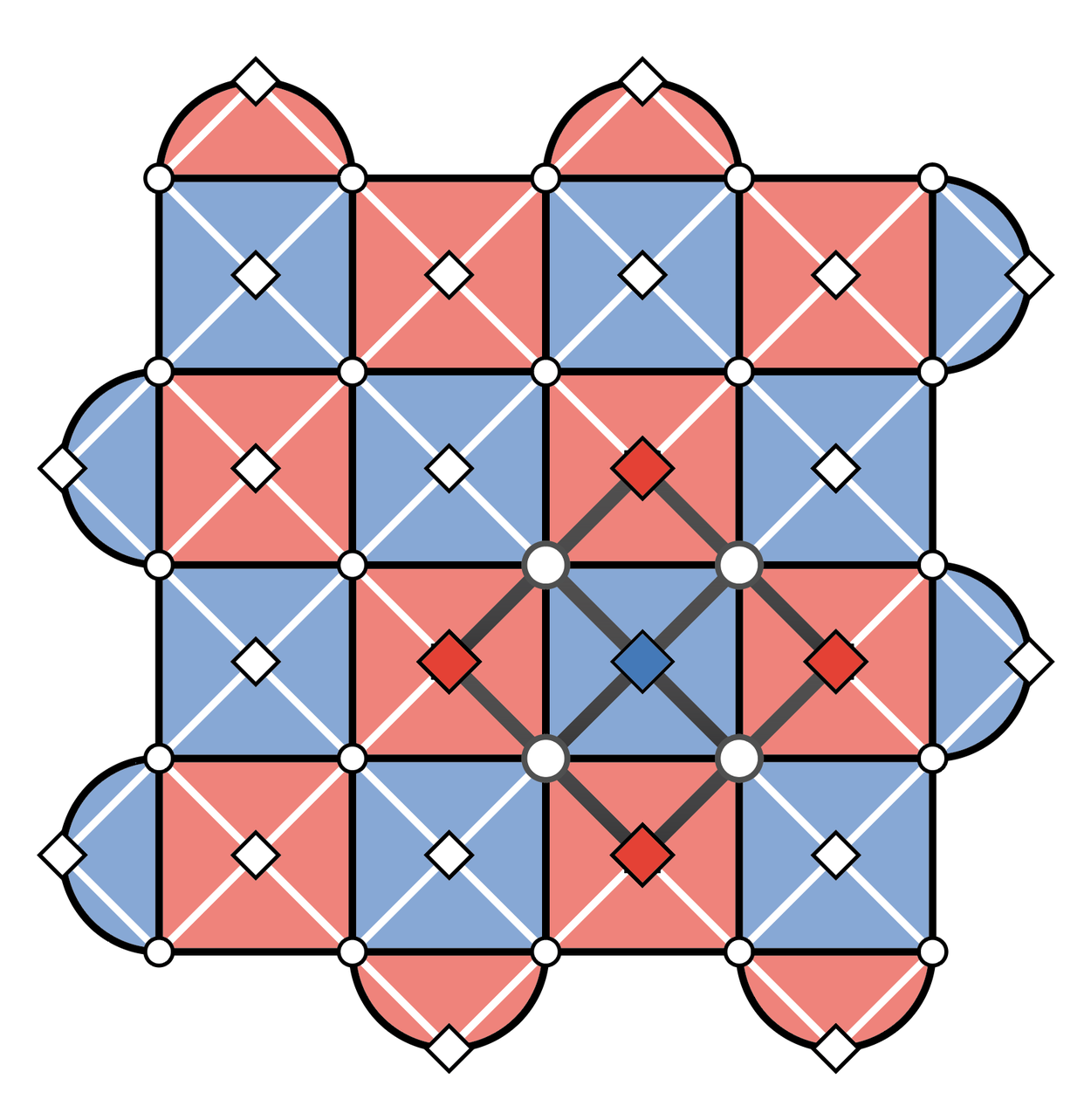
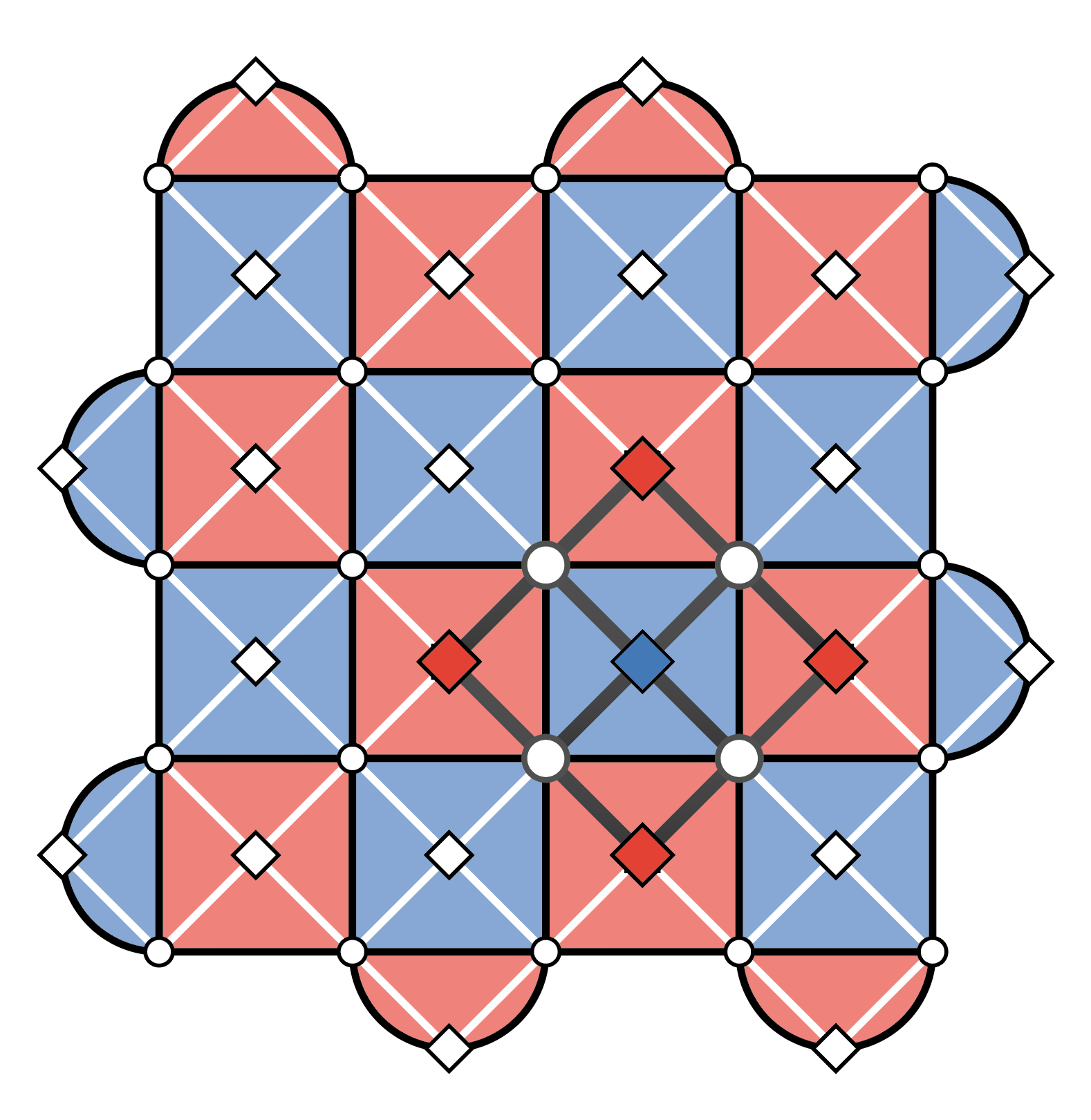
A distance-5 surface code. Each circle represents a data qubit, each diamond a measure qubit, and the qubits are connected on a square lattice.
Today in “Demonstration of dynamic surface codes”, recently published in Nature Physics, we are excited to report the experimental demonstration of a surface code operating with dynamic circuits. Unlike their static counterparts, these dynamic circuits detect errors by alternating between different circuit constructions, which provides greater flexibility in our choice of the types of gates, connectivity, and correlated error suppression. Using dynamic circuits allows us to sidestep some of the big challenges that superconducting qubits face, like leakage out of the computational subspace, hardware layout constraints, and qubit dropouts.
Physical errors are triangulated using detecting regions
The core principle of QEC is to flag physical errors while not destabilizing the underlying logical quantum information. QEC circuits contain measurements that can localize physical errors to a "detecting region", containing a few qubits over a few QEC cycles. In other words, when an error is flagged, the detecting region specifies where and when that error could have occured. By combining many overlapping detecting regions, we can narrow down the location of physical errors and prevent any impact on the logical quantum information. In standard surface code circuits, these detecting regions form a square tiling.
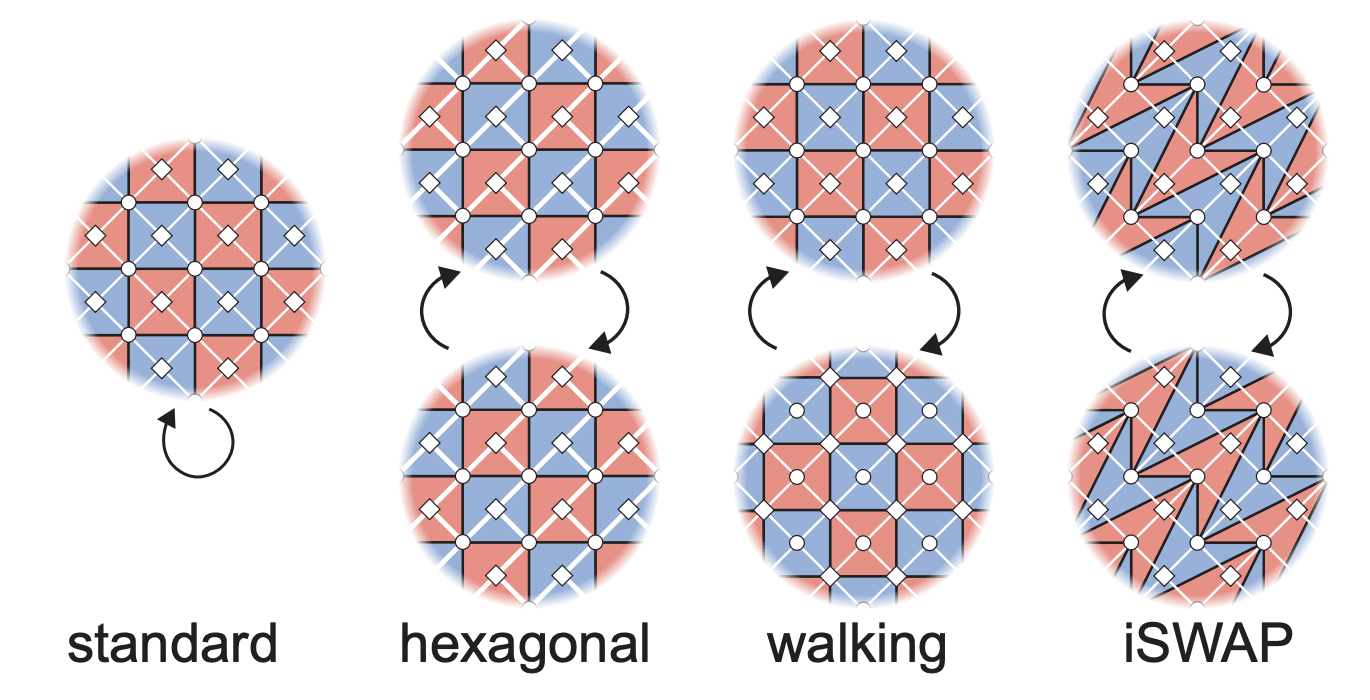
Error correction circuits deform these detecting regions in spacetime. In the standard code, the detecting region tiling always returns to its starting point. In dynamic codes, the tiling of detecting regions changes each cycle. As expanded upon below, we demonstrated three new circuits featuring this periodic re-tiling of the detecting regions: hexagonal, walking, and iSWAP. Each of these three circuits solves a unique challenge in QEC: hexagonal circuits reduce the number of couplers, walking circuits limit non-computation errors, and iSWAP circuits allow use of non-standard two-qubit entangling gates. Together, these demonstrations open the door to a variety of dynamic circuits, including those that avoid dropouts.
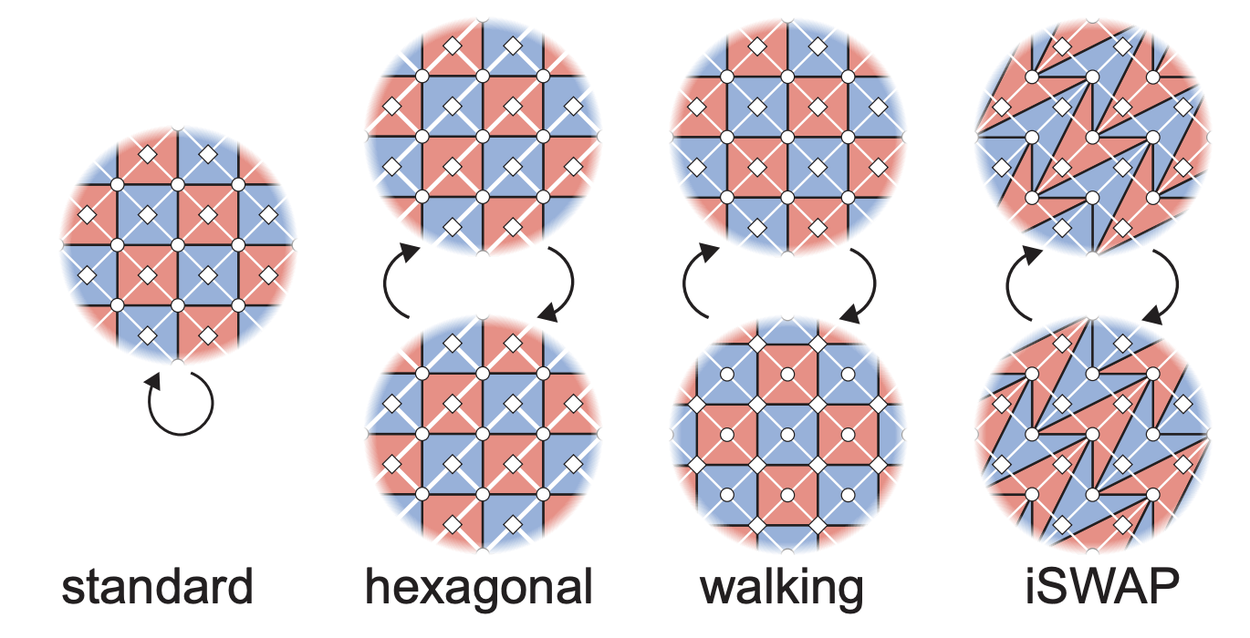
The red and blue shaded regions represent detecting regions at the end of a QEC cycle. While a standard circuit uses a static end-cycle tiling, our dynamic circuits each alternate between two distinct tilings.
Quantum error correction on a hexagonal lattice
In our Willow architecture, each physical qubit is connected to its four nearest neighbors, forming a square lattice. This arrangement of connections allows gates between the neighboring qubits, but also introduces design constraints, such as the overhead of extra wires needed to control couplers between qubits. Realizing error correction instead on a hexagonal lattice would permit each qubit to connect with only three neighbors instead of four, thereby simplifying the design and fabrication process of these large chips and enhancing hardware performance.
To achieve error correction with only three couplers per qubit, we make use of dynamic circuits that feature two distinct types of error correction cycles. Both cycle types leverage three couplers per qubit, with one coupler utilized twice within the cycle. The result is a quantum error correction circuit with dynamic, overlapping detecting regions that can still be used to triangulate errors, but only requiring three couplers per qubit.
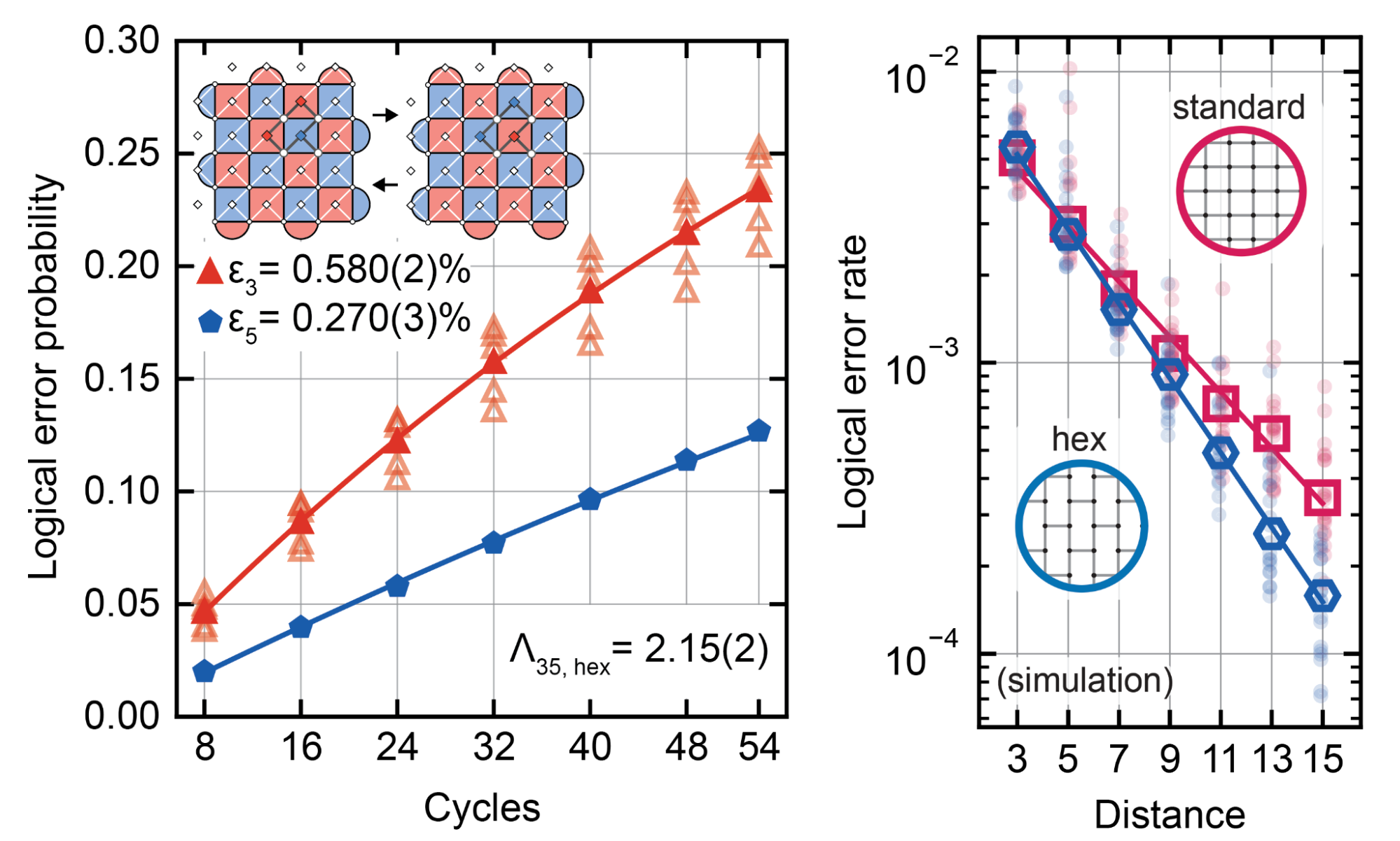
We evaluated this three-coupler error correction circuit on our Willow processor, which has square connectivity. To measure the hexagonal code, we turned off all the unused couplers, to simulate the performance of hexagonal connectivity. We found that as the code's distance scales from 3 to 5, the logical error rate improves by a factor of 2.15, matching the performance of a traditional static circuit operating on the same hardware that we presented in our milestone experiment last year.
Our findings demonstrate the feasibility of constructing a hexagonal qubit lattice for quantum error correction, a design space we thoroughly investigated in simulation. By adopting a hexagonal lattice, we can significantly reduce the complexity of our optimization algorithms for selecting qubit and gate frequencies. This simplification leads to a 15% improvement in the simulated error suppression factor, showcasing the novel capabilities unlocked by designing a processor with three couplers per qubit, rather than four.
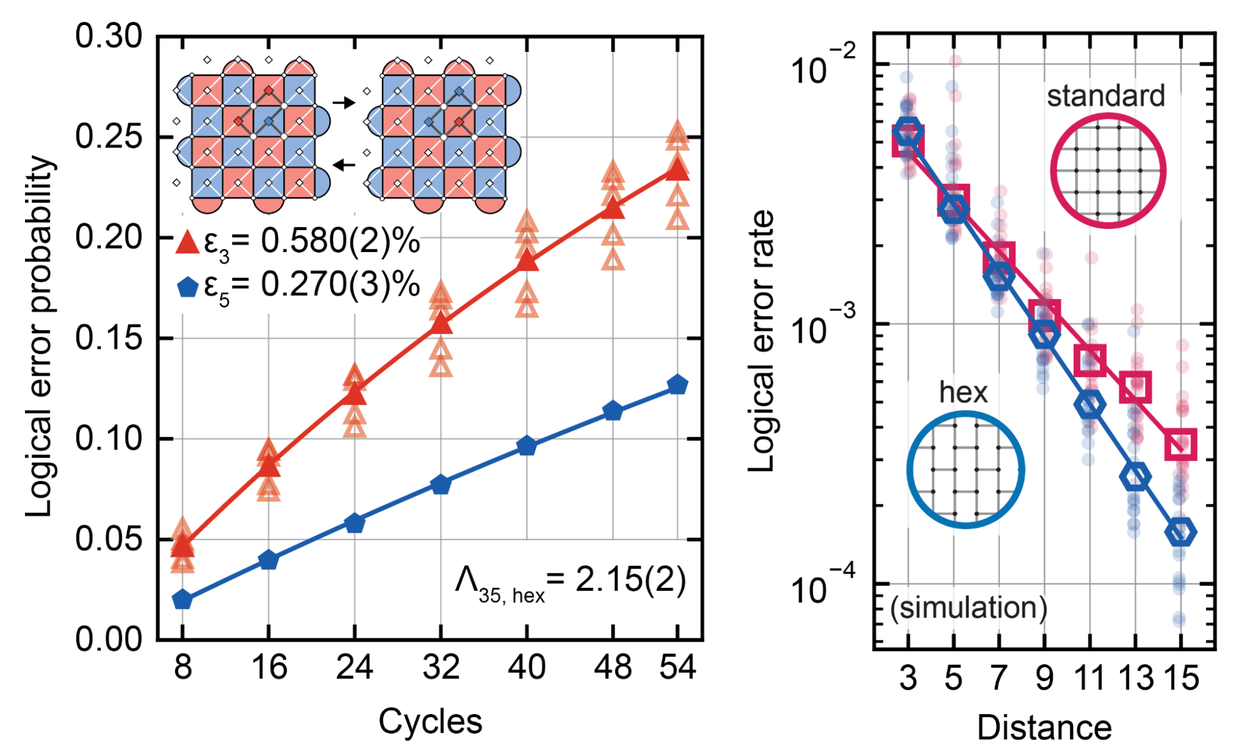
Left: Error correction performance of the hexagonal dynamic circuit on our Willow processor for distance-3 (red) and distance-5 (blue) codes. Right: Simulated comparison between a hexagonal lattice (blue) and a square lattice (red) for quantum error correction.
Exchanging the roles of data and measure qubits
While a qubit is fundamentally defined by its two quantum states, |0⟩ and |1⟩, our physical superconducting circuits possess additional, higher-energy states not utilized in computation or error correction. When a qubit escapes into these higher-energy states — a phenomenon known as leakage — it can induce correlated errors, diminishing the efficacy of quantum error correction. We can remove this leakage on measure qubits using a leakage reset technique, and we’ve shown it can be removed on data qubits using a special sequence of gates called data-qubit-leakage-removal (DQLR). However, such DQLR introduces new gates into the circuit, adding complexity and additional sources of possible errors.
Using dynamic circuits, we can instead realize error correction with a circuit that periodically swaps the role of “data” and “measure” qubits. In this way, the simple leakage reset applied to measure qubits can now be applied to all qubits, without any additional gates in the QEC cycle. We call this periodic swapping of qubits a walking circuit, since it allows a logical qubit to move across the device, wiggling back-and-forth in the process.
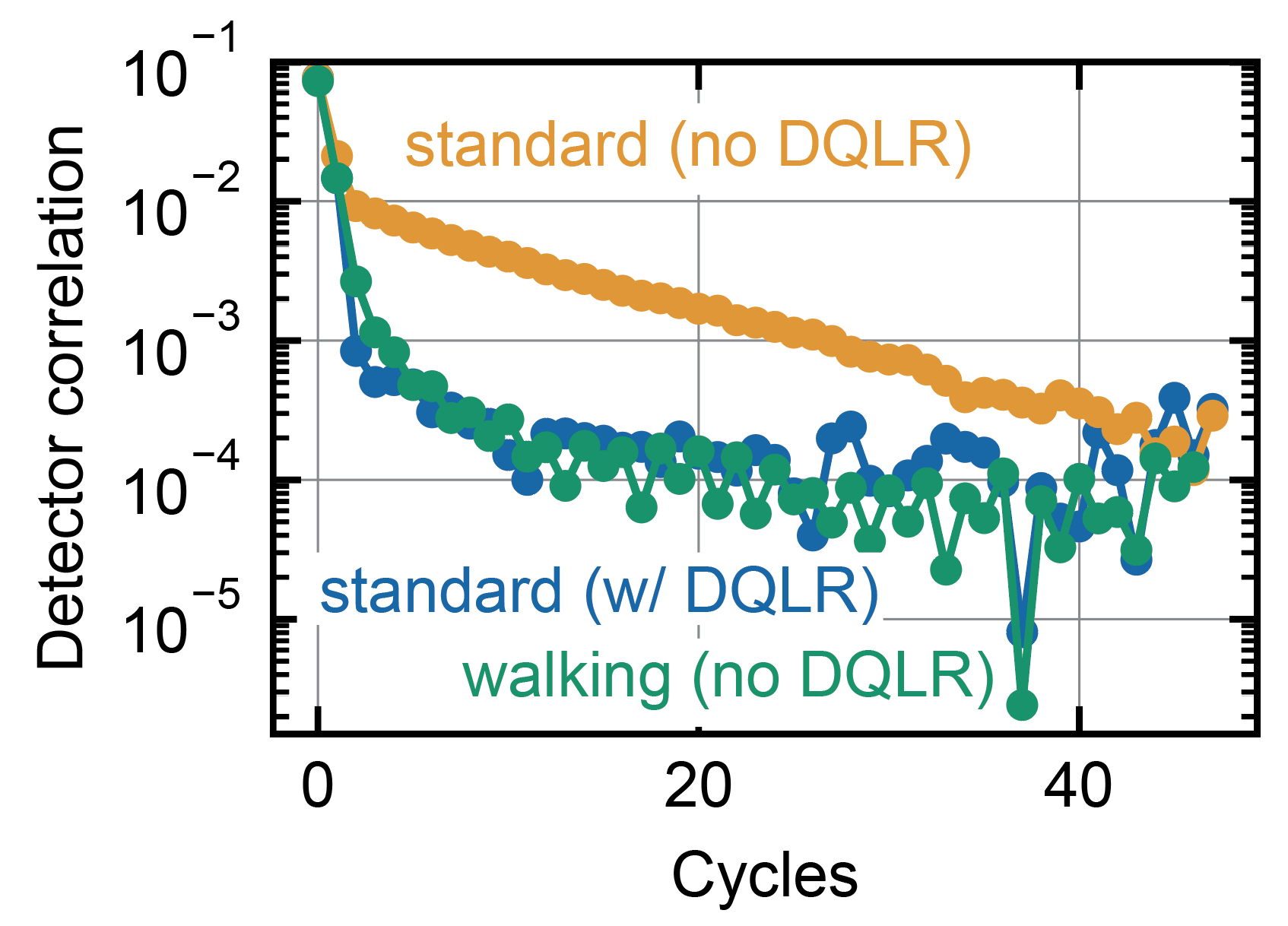
Below we show how our walking circuit can reduce additional correlated errors caused by leakage. The plotted points represent how detectors separated by many cycles are correlated, with lower values signaling fewer correlated errors. In our standard circuit, these correlations remain for up to 40 cycles. By using walking (green), we significantly reduce these correlations by over an order of magnitude. Moreover, this level of suppression matches our standard surface code, using the DQLR technique.
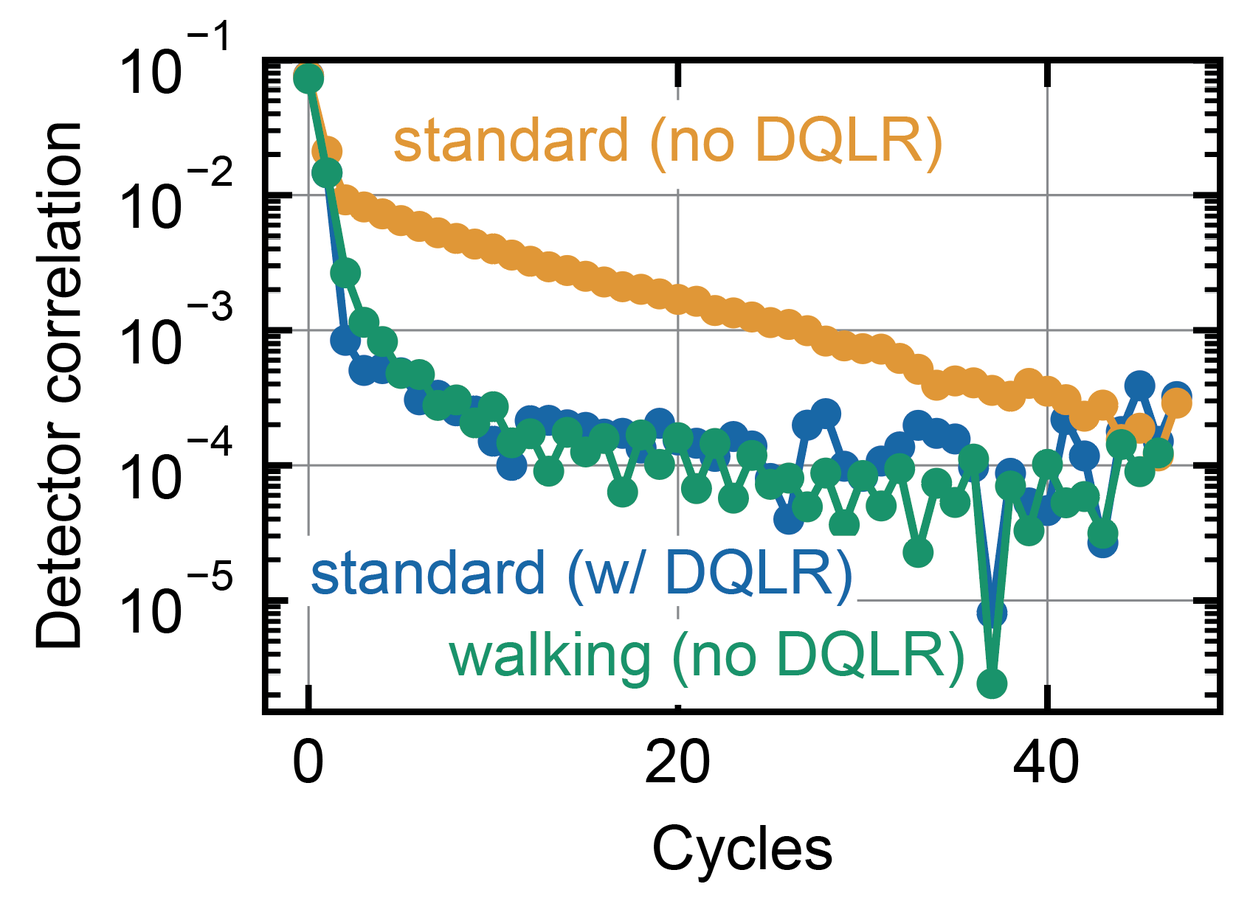
Time-correlated errors measured in different error correction circuits (lower is better).
Make way for the iSWAP gate
In traditional circuits for error correction of the surface code, the controlled-Z (CZ) gate is used to entangle data and measure qubits. However, in our recent demonstration of a verifiable quantum advantage, we’ve used a different type of quantum gate, called the iSWAP gate. This iSWAP gate swaps the qubit states while also performing a controlled-Z (CZ) operation. Unlike the CZ gate, the iSWAP gate does not rely on non-computational states for its realization. As a result, the iSWAP gate generates fewer correlated errors caused by leakage.
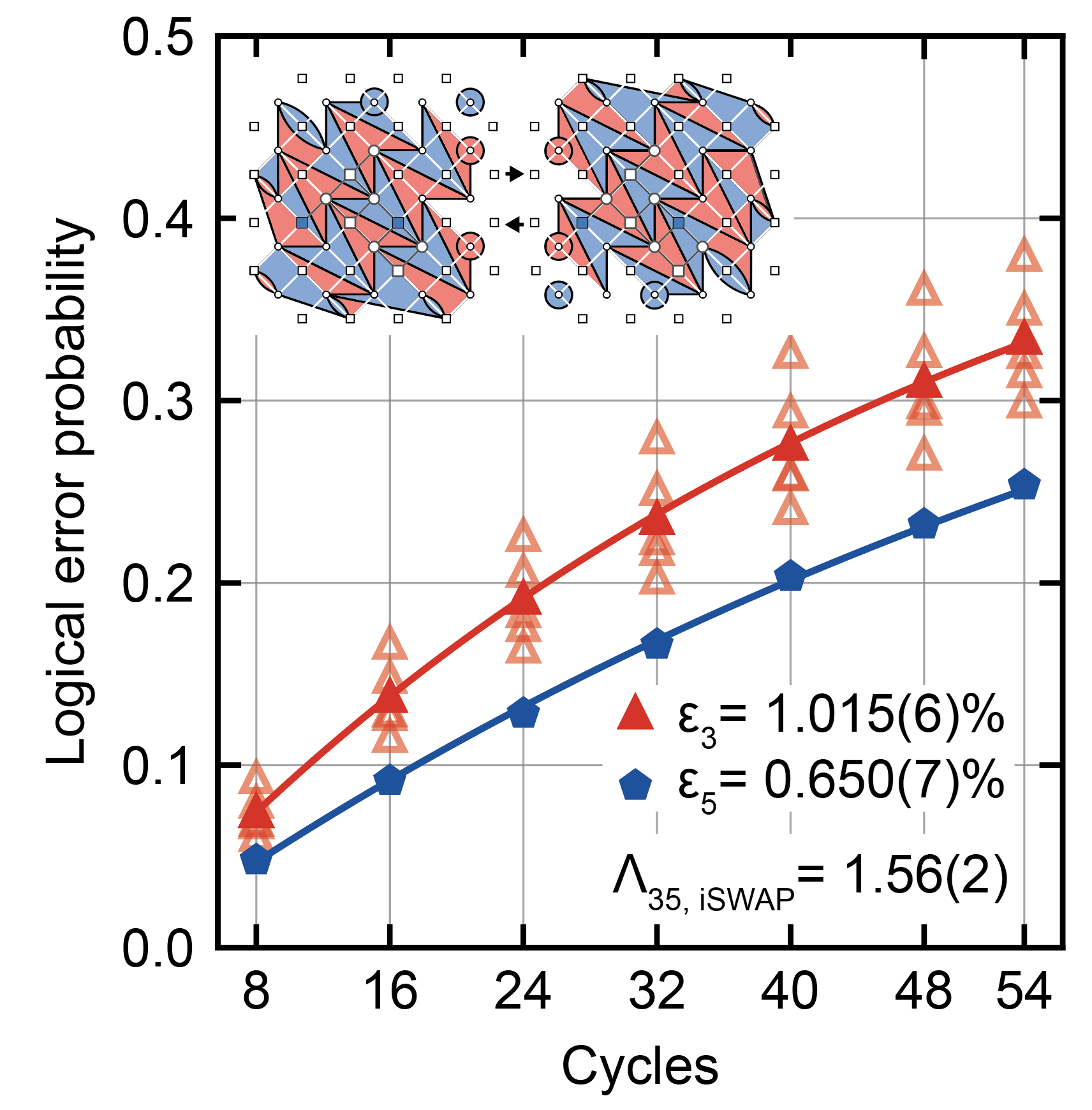
The superior properties of the iSWAP gate raises the question: can the iSWAP gate be used for quantum error correction instead of the CZ gate? As shown in our prior theory work, the iSWAP gate can be used in a dynamic circuit to realize error correction of the surface code. We demonstrate such a circuit on our Willow superconducting processor, achieving a strong error suppression factor of 1.56. This performance is slightly below that of a standard circuit using CZ gates as our device was designed and optimized for CZ gate error correction, but our demonstration of this iSWAP code confirms the viability of the iSWAP gate for error correction, paving the way for future device designs optimized for this gate.
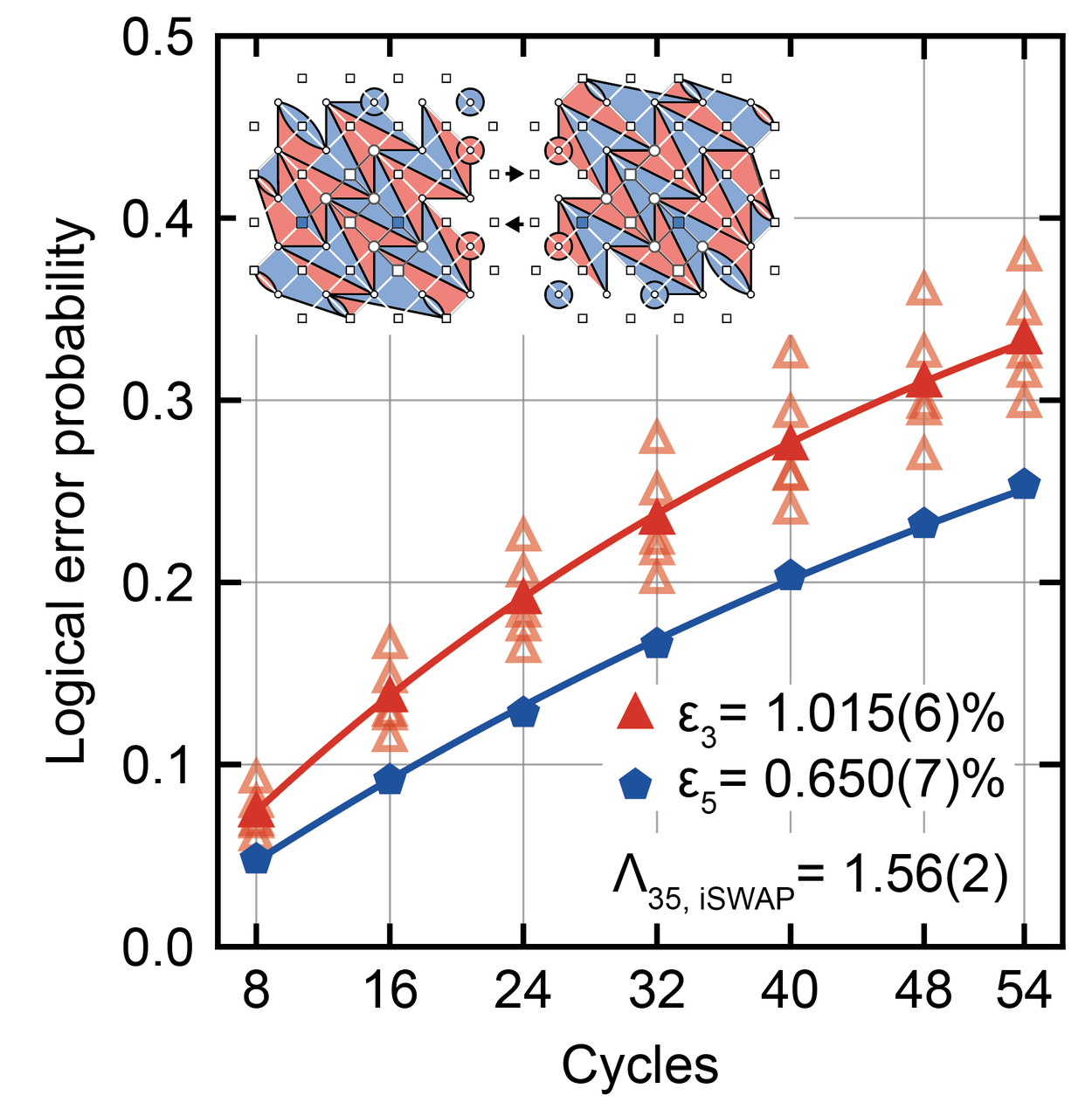
Error correction performance of the iSWAP code on our Willow processor.
What’s next
Our error correction demonstrations prove that dynamic circuits are a viable approach to fault tolerance. By relaxing the constraints on connectivity and expanding viable gate sets, dynamic circuits open new avenues for co-designing quantum hardware and error correction protocols. A notable advantage of these dynamic circuits is their capacity to circumvent "dropouts" within our quantum error-correcting codes, a phenomenon where certain qubits or couplers experience failure.
These demonstrations, alongside our recent color code operation on the Willow architecture, firmly establish the viability of error correction beyond the conventional static surface code model. Our results push us closer to our next milestone: a long-lived logical qubit with an error rate of less than one error per million cycles of error correction.
Acknowledgments
The primary contributors to this work are Alec Eickbusch, Matt McEwen, and Alexis Morvan.
-
Labels:
- Quantum