Do Wide and Deep Networks Learn the Same Things?

A common practice to improve a neural network’s performance and tailor it to available computational resources is to adjust the architecture depth and width. Indeed, popular families of neural networks, including EfficientNet, ResNet and Transformers, consist of a set of architectures of flexible depths and widths. However, beyond the effect on accuracy, there is limited understanding of how these fundamental choices of architecture design affect the model, such as the impact on its internal representations.

In “Do Wide and Deep Networks Learn the Same Things? Uncovering How Neural Network Representations Vary with Width and Depth”, we perform a systematic study of the similarity between wide and deep networks from the same architectural family through the lens of their hidden representations and final outputs. In very wide or very deep models, we find a characteristic block structure in their internal representations, and establish a connection between this phenomenon and model overparameterization. Comparisons across models demonstrate that those without the block structure show significant similarity between representations in corresponding layers, but those containing the block structure exhibit highly dissimilar representations. These properties of the internal representations in turn translate to systematically different errors at the class and example levels for wide and deep models when they are evaluated on the same test set.

Comparing Representation Similarity with CKA

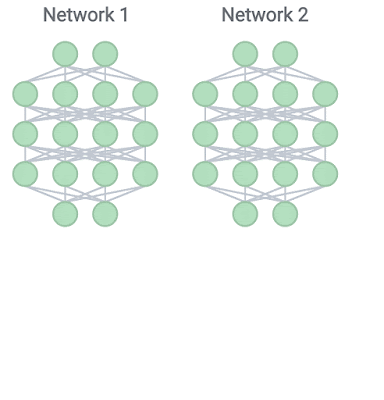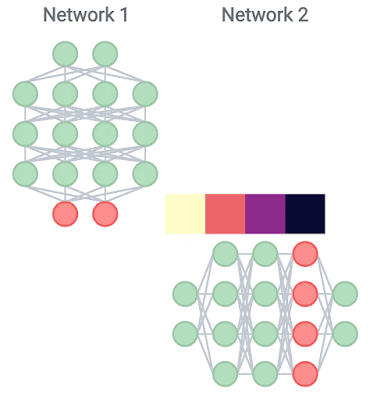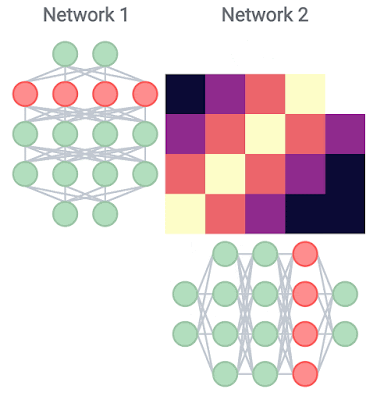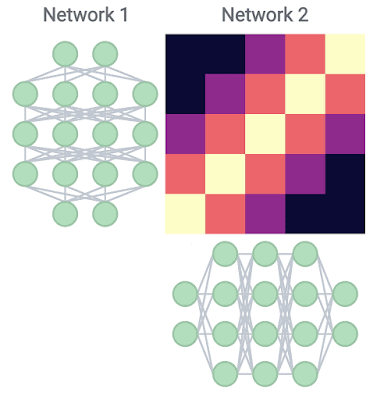
We extended prior work on analyzing representations by leveraging our previously developed Centered Kernel Alignment (CKA) technique, which provides a robust, scalable way to determine the similarity between the representations learned by any pair of neural network layers. CKA takes as input the representations (i.e., the activation matrices) from two layers, and outputs a similarity score between 0 (not at all similar) and 1 (identical representations).

We apply CKA to a family of ResNets of varying depths and widths, trained on common benchmark datasets (CIFAR-10, CIFAR-100 and ImageNet), and use representation heatmaps to illustrate the results. The x and y axes of each heatmap index the layers of the model(s) in consideration, going from input to output, and each entry (i, j) is the CKA similarity score between layer i and layer j.

We use CKA to compute the representation similarity for all pairs of layers within a single model (i.e., when network 1 and network 2 are identical), and across models (i.e., when network 1 and network 2 are trained with different random initializations, or have different architectures altogether).

Below is an example of the resulting heatmap when we compare representations of each layer to every other layer within a single ResNet of depth 26 and width multiplier 1. In the design convention used here, the stated depth only refers to the number of convolutional layers in the network, but we analyze all layers present, and the width multiplier applies to the number of filters in each convolution. Notice the checkerboard pattern in the heatmap, which is caused by skip connections (shortcuts between layers) in the architecture.

The Emergence of the Block Structure

What stands out from the representation heatmaps of deeper or wider networks is the emergence of a large set of consecutive layers with highly similar representations, which appears in the heatmaps as a yellow square (i.e., a region with high CKA scores). This phenomenon, which we call the block structure, suggests that the underlying layers may not be as efficient at progressively refining the network’s representations as we expect. Indeed, we show that the task performance becomes stagnant inside the block structure, and that it is possible to prune some underlying layers without affecting the final performance.

Block structure — a large, contiguous set of layers with highly similar representations — emerges with increasing width or depth. Each heatmap panel shows the CKA similarity between all pairs of layers within a single neural network. While its size and position can vary across different training runs, the block structure is a robust phenomenon that arises consistently in larger models.

With additional experiments, we show that the block structure has less to do with the absolute model size, than with the size of the model relative to the size of the training dataset. As we reduce the training dataset size, the block structure starts to appear in shallower and narrower networks:

With increasing network width (towards the right along each row) and decreasing dataset size (down each column), the relative model capacity (with respect to a given task) is effectively inflated, and the block structure begins to appear in smaller models.

Through further analysis, we are also able to demonstrate that the block structure arises from preserving and propagating the dominant principal components of its underlying representations. Refer to our paper for more details.

Comparing Representations Across Models

Going further, we study the implications of depth and width on representations across models of different random initializations and different architectures, and find that the presence of block structure makes a significant difference in this context as well. Despite having different architectures, wide and deep models without the block structure do exhibit representation similarity with each other, with corresponding layers broadly being of the same proportional depth in the model. However, when the block structure is present, its representations are unique to each model. This suggests that despite having similar overall performance, each wide or deep model with the block structure picks up a unique mapping from the input to the output.

For smaller models (e.g., ResNet-38 1×), CKA across different initializations (off the diagonal) closely resembles CKA within a single model (on the diagonal). In contrast, representations within the block structure of wider and deeper models (e.g., ResNet-38 10×, ResNet-164 1×) are highly dissimilar across training runs.

Error Analysis of Wide and Deep Models

Having explored the properties of the learned representations of wide and deep models, we next turn to understanding how they influence the diversity of the output predictions. We train populations of networks of different architectures and determine on which test set examples each architecture configuration tends to make errors.

On both CIFAR-10 and ImageNet datasets, wide and deep models that have the same average accuracy still demonstrate statistically significant differences in example-level predictions. The same observation holds for class-level errors on ImageNet, with wide models exhibiting a small advantage in identifying classes corresponding to scenes, and deep networks being relatively more accurate on consumer goods.

Per-class differences on ImageNet between models with increased width (y-axis) or depth (x-axis). Orange dots reflect differences between two sets of 50 different random initializations of ResNet-83 (1×).

Conclusions

In studying the effects of depth and width on internal representations, we uncover a block structure phenomenon, and demonstrate its connection to model capacity. We also show that wide and deep models exhibit systematic output differences at class and example levels. Check out the paper for full details on these results and additional insights! We’re excited about the many interesting open questions these findings suggest, such as how the block structure arises during training, whether the phenomenon occurs in domains beyond image classification, and ways these insights on internal representations can inform model efficiency and generalization.

Acknowledgements

This is a joint work with Maithra Raghu and Simon Kornblith. We would like to thank Tom Small for the visualizations of the representation heatmap.