Differential privacy on trust graphs
May 13, 2025
Pasin Manurangsi and Serena Wang, Research Scientists, Google Research
We propose a new model for differential privacy that incorporates different trust assumptions between users, and devise several algorithms and lower bounds in this model.
Quick links
Differential privacy (DP) is a mathematically rigorous and widely studied privacy framework that ensures the output of a randomized algorithm remains statistically indistinguishable even if the data of a single user changes. This framework has been extensively studied in both theory and practice, with many applications in analytics and machine learning (e.g., 1, 2, 3, 4, 5, 6, 7).
The two main models of DP are the central model and the local model. In the central model, a trusted curator has access to raw data and is responsible for producing an output that is differentially private. The local model requires that all messages sent from a user’s device are themselves differentially private, removing the need for a trusted curator. While the local model is appealing due to its minimal trust requirements, it often comes with significantly higher utility degradation compared to the central model.
In real-world data-sharing scenarios, users often place varying levels of trust in others, depending on their relationships. For instance, someone might feel comfortable sharing their location data with family or close friends but would hesitate to allow strangers to access the same information. This asymmetry aligns with philosophical views of privacy as control over personal information, where individuals specify with whom they are willing to share their data. Such nuanced privacy preferences highlight the need for frameworks that go beyond the binary trust assumptions of existing differentially private models, accommodating more realistic trust dynamics in privacy-preserving systems.
In “Differential Privacy on Trust Graphs”, published at the Innovations in Theoretical Computer Science Conference (ITCS 2025), we use a trust graph to model relationships, where the vertices represent users, and connected vertices trust each other (see below). We explore how to apply DP to these trust graphs, ensuring that the privacy guarantee applies to messages shared between a user (or their trusted neighbors) and everyone else they do not trust. In particular, the distribution of messages exchanged by each user u or one of their neighbors with any other user not trusted by u should be statistically indistinguishable if the input held by u changes, which we call trust graph DP (TGDP).
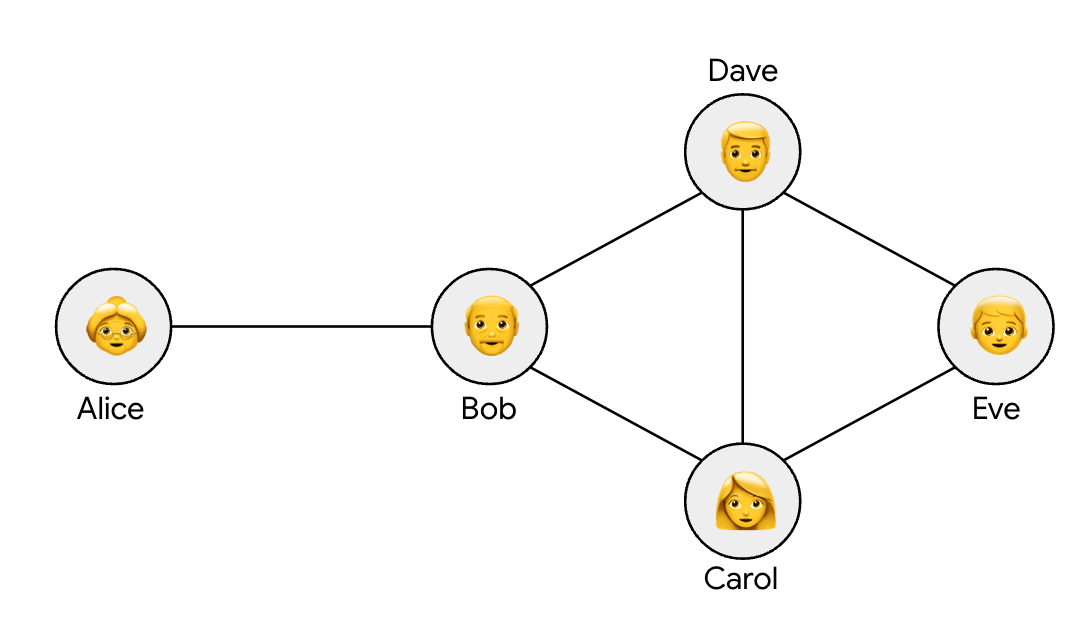
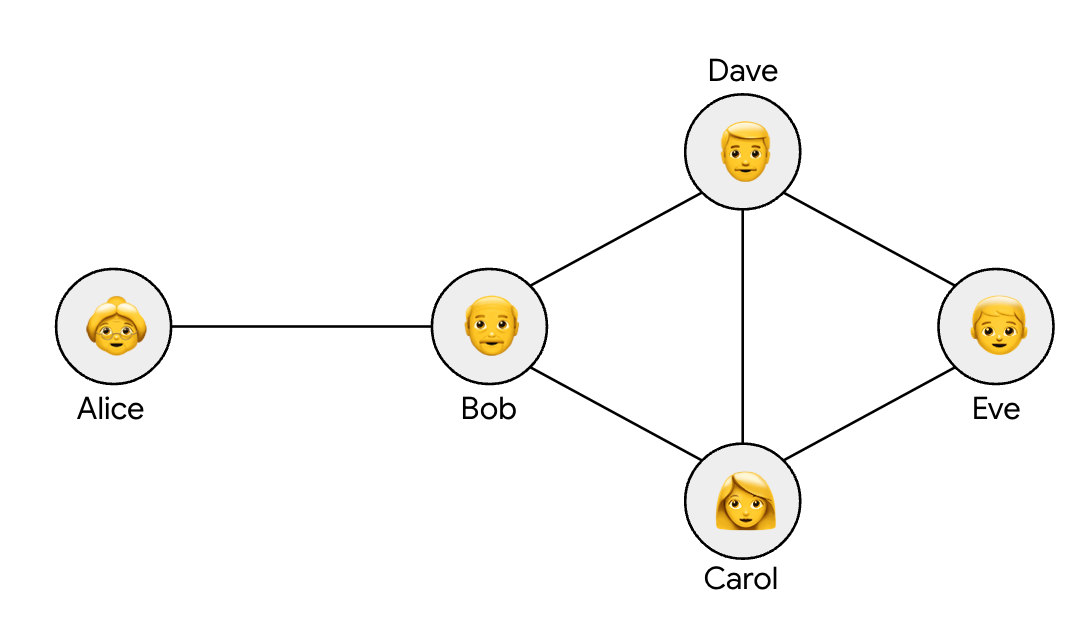
Example of a trust graph with location sharing. Alice shares her location with Bob, who shares his location with Carol and Dave. Carol and Dave share their location with Eve. Under the definition of trust graph DP that we introduce, it is required that Carol, Dave, and Eve cannot identify Alice’s information, even if they pooled together all of their data and any data shared with them.
Trust graph DP
TGDP interpolates between the central and local models in a natural way. The central model is equivalent to TGDP over a star graph, with the trusted central data curator at the center connected to all other users (the top figure, below). The local model, on the other hand, is equivalent to TGDP over a fully unconnected graph, in which no users trust any other users (the bottom figure, below).
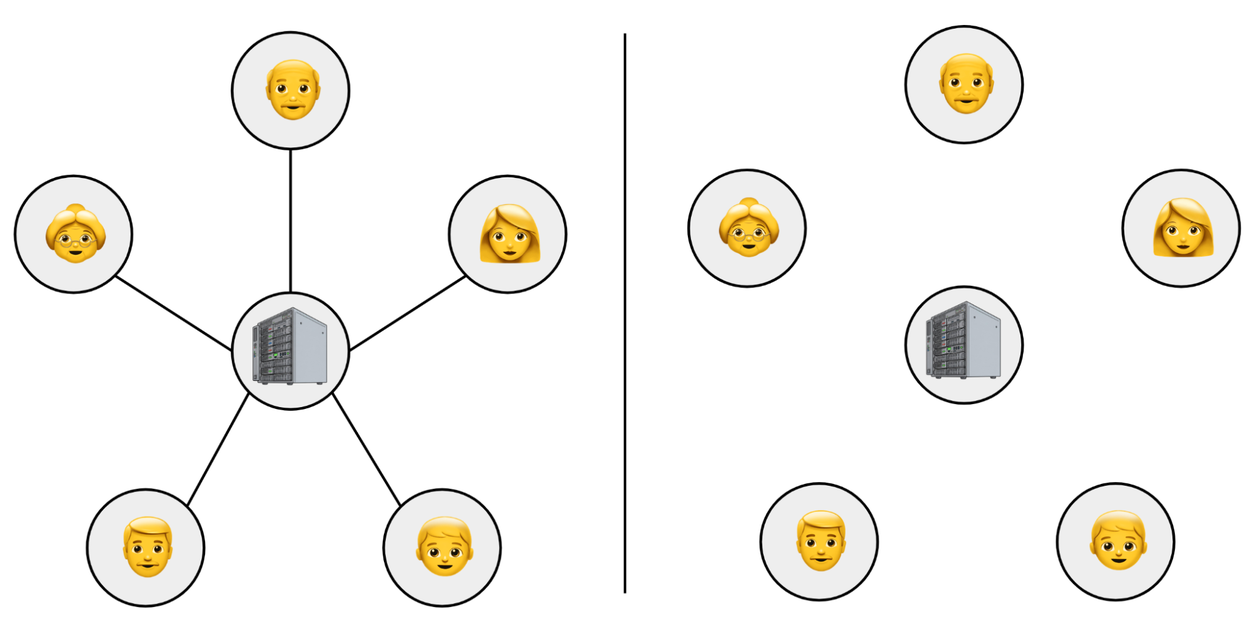
Left: Example of a “star” trust graph that corresponds with the central model of DP, in which all users trust a central curator. Right: Example of a fully unconnected trust graph that corresponds with the local model of DP, in which no users trust any other users.
It is known that algorithms that must satisfy central DP can be more accurate than algorithms that must satisfy local DP, since there is more flexibility to share data under central DP. With TGDP, we can quantify algorithm accuracy under more general trust relationships in between.
We quantify accuracy specifically through a simple aggregation task, which is a building block to more complicated machine learning tasks. Suppose each user has a private data value, xi, which is a real number bounded within some range. The goal of the aggregation task is to devise an algorithm that can estimate the sum of all users’ values, Σi xi, with as low error as possible (measured as mean-squared error).
In the next sections, we provide both upper and lower bounds on the error of algorithms for aggregation that satisfy TGDP. These bounds quantify the limits of TGDP algorithms: one can do at least as well as the upper bound, and no TGDP algorithm can do better than the lower bound.
An algorithm based on dominating set
We provide an algorithm for aggregation that satisfies TGDP. Both the algorithm and the upper bound rely on a dominating set of the trust graph.
A dominating set T is a subset of graph vertices such that every vertex not in T is adjacent to at least one vertex in T. For example, the figure below shows a dominating set in blue.
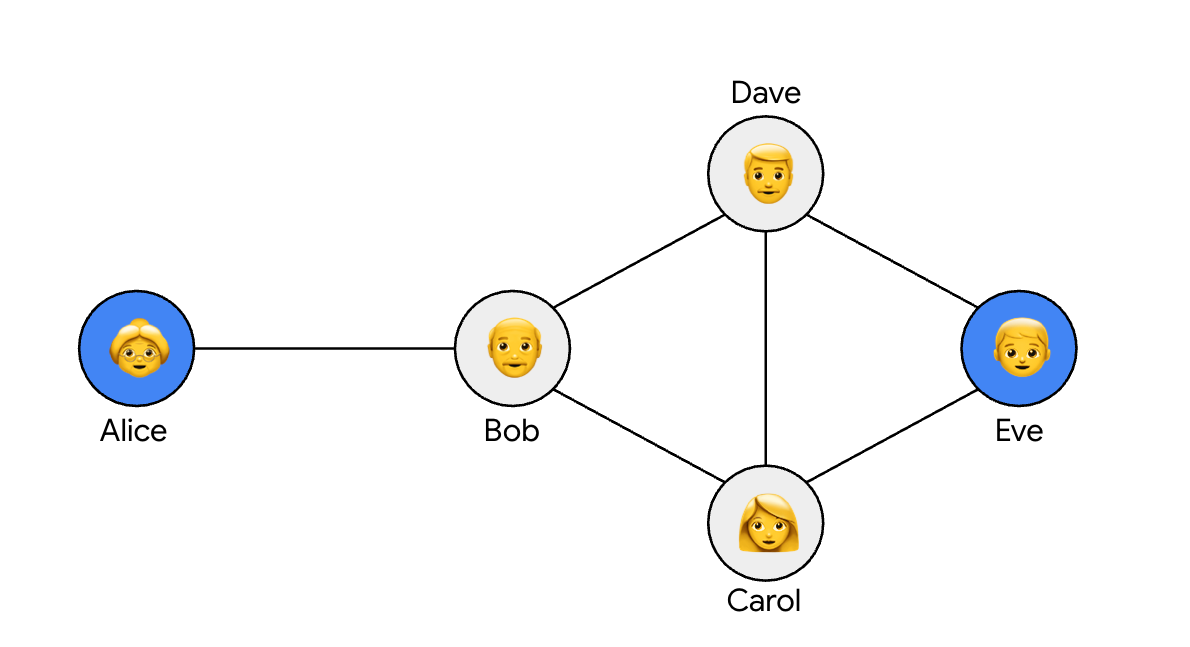
Illustration of a dominating set in a trust graph. Alice and Eve, highlighted in blue, are part of the dominating set T.
By definition of a dominating set, every user trusts at least one user in the set. This allows us to build an algorithm by letting each user send their raw data to their trusted neighbor in the set, after which the trusted neighbor can aggregate all data it receives and add an appropriate noise to achieve differential privacy. More specifically, our dominating set algorithm works as follows:
- Find a dominating set T of the trust graph.
- Each user sends their data to a neighbor in the dominating set T.
- Each user in the dominating set T broadcasts the sum of all numbers it receives plus Laplace noise.
- The estimate is the sum of all noisy broadcasts.
The error of this algorithm is no greater than a function of the size of the dominating set T. This error is minimized for the smallest possible dominating set, or the minimum dominating set. The size of the minimum dominating set in a graph G is called its domination number.
Thus, if we are able to find the minimum dominating set in step 1 above, then the dominating set algorithm can have error at most a constant times the domination number.
A natural question is whether the dominating set algorithm is the best algorithm. It turns out that we can actually do better using linear programming, and we give a better algorithm and upper bound in the paper.
A lower bound via packing number
More generally, we need a lower bound to characterize what the best possible error could be. It turns out that there’s a fairly intuitive lower bound that depends on the packing number of the graph: the maximum size of a set of vertices that share no neighbors.
For example, for the graph in the first figure, the packing number is 2, since Alice and Eve do not share any neighbors. For the star graph, the packing number is 1.
While the dominating set algorithm in the previous section had error upper bounded by the domination number, we prove in the paper that no algorithm can possibly have error smaller than some constant times the packing number.
In general, the domination number is always greater than or equal to the packing number (see e.g., this paper), but there can be a gap. For example, below is a graph with a domination number of 4 and a packing number of 1.
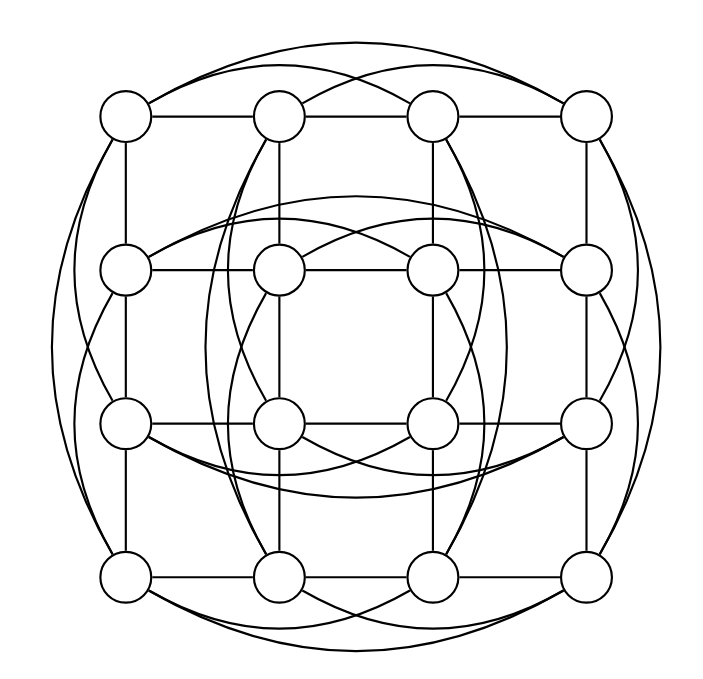
Graph with a gap between the domination number (4) and the packing number (1).
The gap between the domination number and the packing number implies that there is a gap between the upper bound and lower bound on error that we’ve shown here (in the full paper we give an even better upper bound using a linear programming based algorithm, but a gap is still there). Closing this gap between the upper and lower bounds is an open problem in the theory of TGDP algorithms.
ML with trust graph DP
The above dominating set protocol can be easily adapted to aggregate vectors instead of real-numbers. Vector aggregation is a key task in federated analytics and federated learning; for ML applications, vector aggregation can be used to compute the aggregated gradients across different devices. When performing this step with differential privacy, we also get that the final model satisfies differential privacy. This has been the main paradigm for achieving differential privacy in federated learning. Our approach naturally fits into this framework: by using vector aggregation with TGDP, we immediately get that the final ML model satisfies TGDP.
Conclusion
In this work, we introduce trust graph DP (TGDP), a new model for distributed DP which allows a finer-grained control of the trust assumption of each participant. Our TGDP model interpolates between central DP and local DP, allowing us to reason more generally about how trust relationships relate to algorithm accuracy in DP. We provided an algorithm and a lower bound for the aggregation problem. As mentioned above, an interesting open theoretical question is to close the gap between our upper and lower bounds. Our definition may be of practical interest as platforms move towards varied models of trust, from data sharing initiatives in healthcare, to individual data sharing choices on social platforms.
Acknowledgments
This blog post is based on joint work with Badih Ghazi and Ravi Kumar. We also thank them for providing us with helpful feedback during the preparation of this blog post.





