Can algorithms make tournament cheating obsolete?
November 13, 2024
Ariel Schvartzman, Research Scientist, Google Research, Athena Team
We create a tournament rule that attempts to satisfy three key criteria required to make it pointless for teams to collude or match-fix. We find that it’s impossible to develop a rule that satisfies all three criteria but also that team selfishness usually prevents collusion in the first place.
Tournament cheating is often seen in films and books, but happens rarely in real life. Nevertheless, there are some high-profile examples with wide-ranging impact. Thus, it’s useful to examine ways sports tournament organizers could structure their tournament rules to reduce or even eliminate incentives to cheat. In fact, some of the algorithmic approaches commonly used in computer science research are particularly suited for a specific type of sports collusion: the one where teams realize that they can help their team (or teams) by losing on purpose.
Depending on the points system used, round-robin (where every team plays each other once) and seeding-based tournaments open the possibility for teams to purposely lose for the sake of helping another team advance, or for the sake of helping each other advance simultaneously.
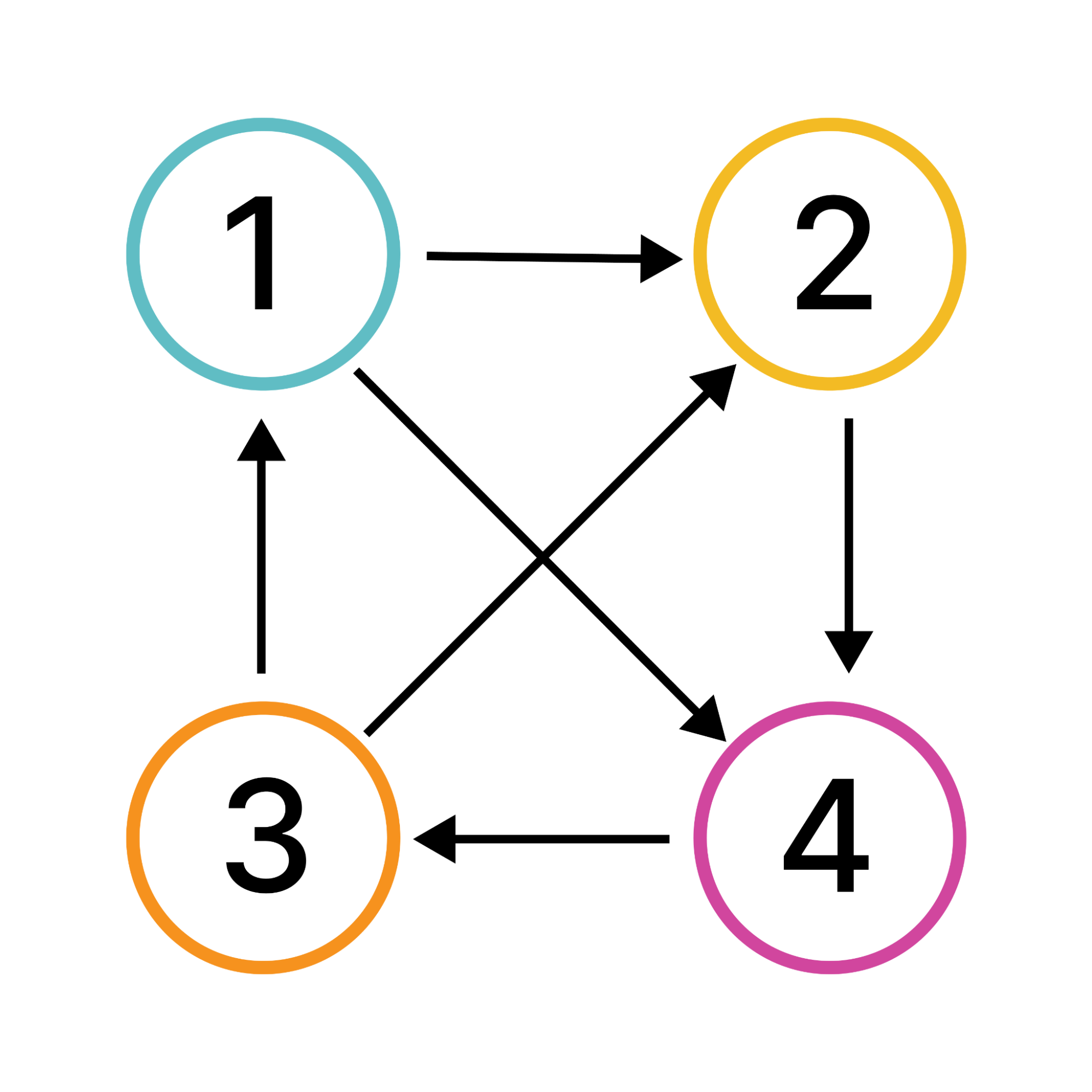
“Tournament” is of course a common sports term, but it’s also a term in graph theory describing models with pairwise relationships between connected objects, and this happens to apply directly to the way sports tournaments work.
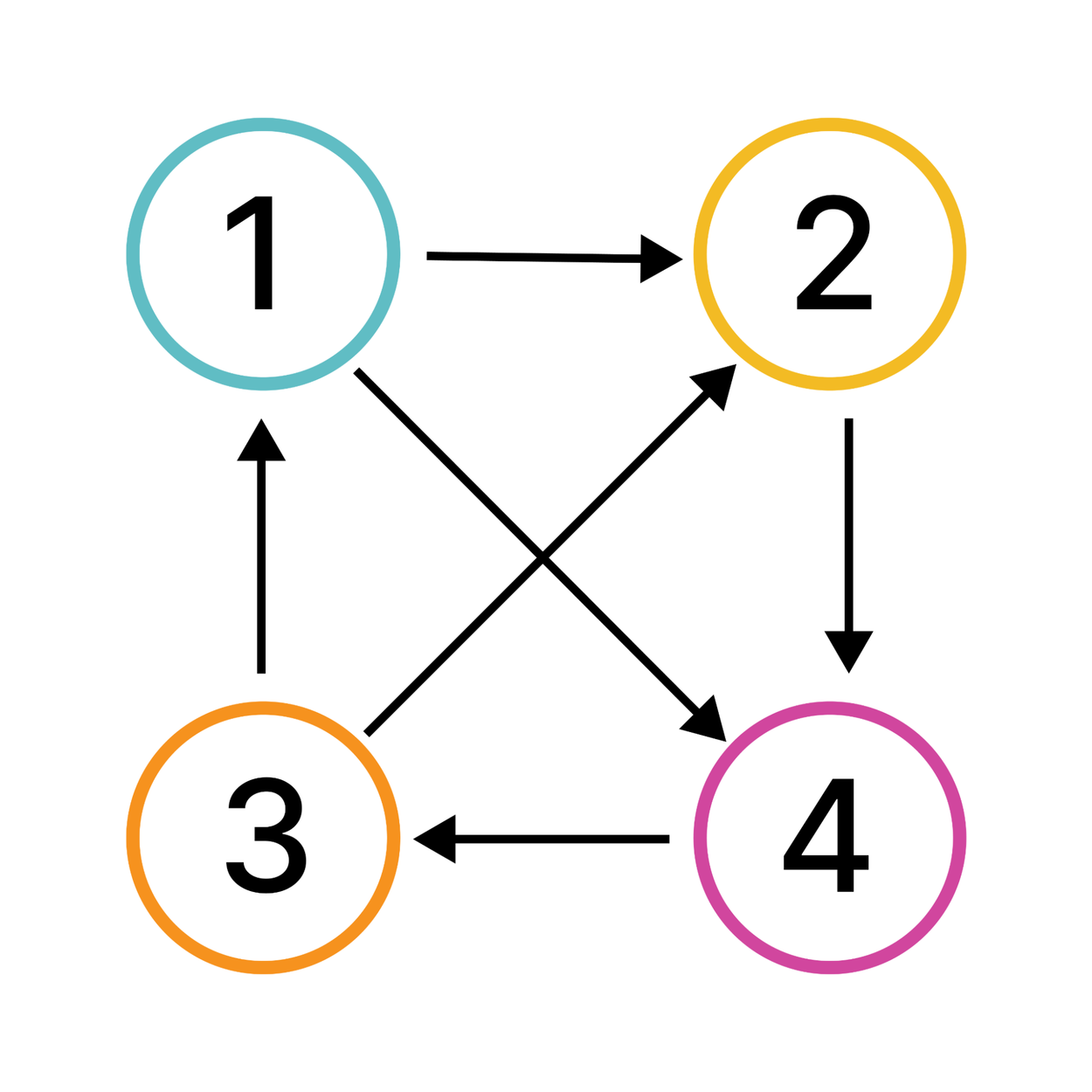
A tournament on four vertices.
Suppose you organize a tournament where each team plays each other once and ties aren’t allowed. This would look like a tournament graph in which every team pair is connected by a line with an arrow pointing to the loser of the match between those teams. To devise a totally fair tournament that makes colluding or losing on purpose pointless, the rules around deciding who the winner is should align with the following three desired properties:
- The team that beats every other team is the winner of the whole tournament, if it exists.
- Every team is incentivized to win every game.
- Teams don’t benefit from forming match-fixing coalitions.
In “On Approximately Strategy-Proof Tournament Rules for Collusions of Size at Least Three”, we set out to devise a tournament rule that satisfies properties 1 and 2 above, as well as a relaxed version of 3. Then, in “Toward Fair and Strategyproof Tournament Rules for Tournaments with Partially Transferable Utilities”, we sought to create a tournament model that accepts and deals with the mathematical impossibility of satisfying both 1 and 3 by assuming and incorporating degrees of selfishness on the part of each team. We show that no fair tournament rule can prevent manipulations if the potential gain from colluding is greater than the team’s degree of selfishness times its individual sacrifice, and we computationally solve for fair (meaning it satisfies properties 1 and 2 above) and manipulation-resistant tournament rules according to the selfishness parameter for a small number of teams.
Designing the rules
Before we could design rules and test them against our desired properties, we needed to establish a mathematical language for choosing a winner and changing a tournament’s outcome. We sought to create a tournament rule, that is a way to choose a winner based on outcomes, that makes collusion obsolete. We also assumed that we have observed the outcome of all games played out in a round-robin style tournament.
Suppose a subset of teams (S) wants to fix matches in a tournament (T). We then assume that the only matches that the teams in S can fix are those where both teams playing are in S. “S-adjacent” tournaments are tournaments where all matches involving non-S teams had the same outcome.
With this established, we rephrased the three aforementioned desired properties:
- If there is a team that beats all other teams, assign that team a 100% probability of winning.
- It’s impossible for a team to benefit from losing on purpose.
- The combined chances of any subset of teams winning should be the same in T1 and T2 for any subset of at least two teams, for any two S-adjacent tournaments.
Results
It is easy to find rules that satisfy two of the three desired properties. However, you can satisfy rules 3 or 1 separately but not at the same time. For example, a rule that gives every team 1/(n(n - 1)/2) chance of winning for each game they have won can satisfy properties 2 and 3, but, strangely, it then results in undefeated teams having a less than 100% chance of winning, which violates property 1. Alternatively, we could pick an undefeated team as the winner if there was one and choose a winning team at random (granted, this would also be a strange rule) if there wasn’t. This would satisfy properties 1 and 2, but not 3; there are pairs of tournaments where teams can collude to make one of them an undefeated team, which would boost the groups’ chances of winning from not much better than random to 100%. An instance of this is shown below, wherein picking a different type of rule satisfies these properties in different ways.
An illustration of a pair of (red-blue)-adjacent tournaments. The size of the circles indicate the proportion of wins. When red beats blue, there is a clear winner (the arrow direction goes from the winner to the loser) But when blue beats red, there is no obvious winner, underscoring the importance of designing rules to choose a winner.
We looked at rules that are popular both in theory and practice in search of one that satisfies our requirements but discovered that itIis mathematically impossible to design rules that satisfy properties 1 and 3, even allowing for randomized rules.
Making accommodations
In light of the mathematical impossibility of satisfying all three desired properties, one could try to find rules that satisfy properties 1 and 2 (and maybe some other desirable properties), while minimally breaking property 3. Consider the following way to choose a winner: after observing all matches, draw a random single-elimination bracket (shown below) and fill in the bracket with the results of the observed outcomes until you produce a winner. Prior work has shown this rule satisfies properties 1 and 2 while only minimally violating property 3 for colluding sets of size 2. Violations of property 3 are measured by the worst-case gains from manipulation that violates property 3. In the aforementioned rules, there is at most a 33% greater chance of winning through manipulation. Recently, an explicit rule was proposed that satisfies properties 1 and 2 and suboptimally satisfies property 3 for sets of size 3, meaning that there is a gap between the rule’s guarantees and the worst known case, whose gains from manipulation is at most 51.6%.

A classic sports tournament structure: a single elimination bracket.
Our work proposes a different rule that slightly, but still not optimally, reduces the potential gains from manipulation. The theoretical rule we propose identifies a small set of teams as “significant”, which we define as teams that could form coalitions that lead to a team in the coalition being the clear winner.
We classify each possible tournament outcome into one of five buckets depending on how close it is to having a team win all their games. If the tournament has a team that wins all their games, we declare that team the winner. If the tournament is far from having a team that wins all their games, we choose a winner uniformly at random. For tournaments that are "close" to having a team that wins all their games, we identify those teams that could substantially gain from manipulating the tournament. We prove that there are not many such teams, and for each "close" tournament, we assign specific probabilities to each team so that the gains from manipulation for groups of size three are 50% at most (and still the optimal 33% for groups of size two).
One common concern about our model is that we assume all outcomes of the ground truth are deterministic, e.g., A always beats B, and this may not align with real tournaments. After all, underdogs always have a chance! Do our results hold if we allow for randomized outcomes, e.g., A beats B 80% of the time? It turns out that, thanks to prior work, the answer to this question is “yes” because the worst case instances are those with deterministic outcomes. Related work shows that if we restrict the win probability of all games to, say, the 60–40% interval, then we can expect to decrease the gains from manipulation as the tournament becomes more competitive.
In another attempt to overcome the impossibility result we presented before, we introduce a new model for determining which manipulations are beneficial. In the model outlined thus far, teams in the manipulation coalitions treat their joint probability of winning as a uniform mass. That is, a team in the coalition does not care which other team’s chances of winning go up or down, even if it is their own — an assumption that is unlikely since teams naturally care about their own chance of winning, or are at least a little selfish. To model the assumption that teams in manipulating coalitions are still a little selfish, we introduce weights to the manipulation calculations to reflect this.
We observed that if each team weights their own chances of winning twice as much as that of the other teams in the manipulating coalition, there exist rules that satisfy properties 1 and 3 for tournaments with at most six teams. We conjecture that, under this model, there may indeed exist rules that satisfy properties 1 and 3 exactly. We also show that for several popular rules, a large weight is needed for the rule to satisfy properties 1 and 3.
Conclusion
Many of the popular rules used in sports competitions are highly manipulable, and can actually mirror some of the algorithmic approaches commonly used in computer science research. However, colluding and match-fixing in high-stakes competitions remain rare, suggesting that parts of the model, like considering worst-case instances rather than average-case instances, fail to capture reality. Or perhaps, as our research suggests, teams are sufficiently selfish so that the gains from manipulation are small in comparison to their individual losses, which is why collusion is rare in high-stakes sports competitions.
Acknowledgements
The two research papers discussed in this post are a joint collaboration with Jan Soukup and David Mikšaník, and David Pennock and Eric Xue, respectively. I would also like to acknowledge Jon Schneider, Matt Weinberg, Eitan Zlatin and Albert Zuo, some of whom work at Google now, as collaborators of prior work.



