Bridging the gap in differentially private model training
November 25, 2024
Lynn Chua, Software Engineer, and Pritish Kamath, Research Scientist, Google Research
We identify a gap between the implementation and privacy analysis of a widely used method for private training of neural networks, demonstrate the impact of this gap, and suggest an approach for alleviating its impact.
In today's world, machine learning (ML) models are becoming more ubiquitous. While they provide great utility, such models may sometimes accidentally remember sensitive information from their training data. Differential privacy (DP) offers a rigorous mathematical framework to protect user privacy by injecting "noise" during the model training procedure, making it harder for the model to remember information unique to individual data points. It is desirable to have techniques that provide the best possible model utility at any specified privacy level.
Stochastic gradient descent (SGD) is a commonly used algorithm for training ML models. It works by dividing the data into small mini-batches and updating the model in a sequence of steps based on the data in each batch. A privacy-preserving version, called DP-SGD, adds noise to this learning process to protect individual data points. DP-SGD is widely used for tasks including image classification, ads prediction, generating synthetic data, among others, and is available in popular tools like TensorFlow Privacy, PyTorch Opacus and JAX Privacy.
In “How Private are DP-SGD Implementations?”, presented at ICML 2024, we uncovered a potential privacy vulnerability in how this method is typically implemented. The vulnerability stems from a mismatch between the theoretical assumptions and the practical implementation of how data is randomly divided into mini-batches during training. In “Scalable DP-SGD: Shuffling vs. Poisson Subsampling”, to be presented at NeurIPS 2024, we demonstrate the impact of this vulnerability on private training of neural network models, and we suggest a scalable approach using the Map-Reduce framework for implementing DP-SGD with Poisson subsampling to alleviate this impact.
Vulnerability gap in DP-SGD privacy analysis
Most practical implementations of DP-SGD shuffle the training examples and divide them into fixed-size mini-batches, but directly analyzing the privacy of this process is challenging. Since the mini-batches have a fixed size, if we know that a certain example is in a mini-batch, then other examples have a smaller probability of being in the same mini-batch. Thus, it becomes possible for training examples to leak information about each other.
Consequently, it has become common practice to use privacy analyses that assume that the batches were generated using Poisson subsampling, wherein each example is included in each mini-batch independently with some probability. This allows for viewing the training process as a series of independent steps, making it easier to analyze the overall privacy cost using composition theorems, a widely used methodology in various open-source privacy accounting methods, including those developed by Google and Microsoft. But a natural question arises: is the aforementioned assumption a reasonable one?
The guarantee of differential privacy is quantified in terms of two parameters (ε, δ), which together represent the "privacy cost" of the algorithm. The smaller ε and δ are, the more private the algorithm is. We establish a technique to prove lower bounds on the privacy cost when using shuffling, which means that the algorithm is no more private (that is, the ε, δ values are no smaller) than the bounds that we compute.
In the figure below, we plot the trade-off between the privacy parameter ε and the scale σ of noise applied in DP-SGD, for a fixed number of steps of training (10,000 in this case) and the parameter δ (10-6 in this case). The curve ε𝒟 corresponds to creating the batches without any shuffling or sampling, and the curve ε𝒫 corresponds to DP-SGD with batches using Poisson subsampling. The curve ε𝒮 is obtained using our lower bound technique, showing that for small σ, the actual privacy cost of using DP-SGD with shuffling (orange line, below) can be significantly higher than that of Poisson subsampling (green line).
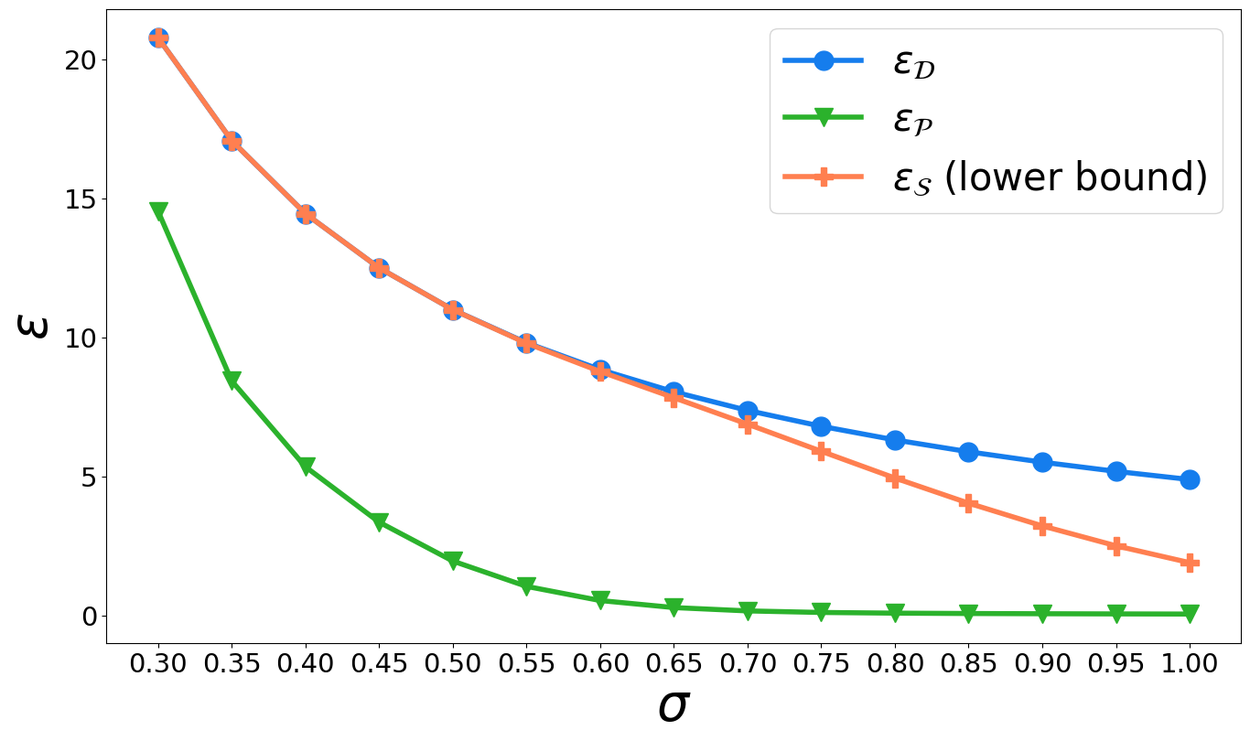
Plot showing how ε varies with the noise scale σ, for a fixed δ and number of steps for different approaches to batch construction.
Implementing Poisson sub-sampling at scale
Poisson subsampling is rarely implemented in practice because it produces variable-size batches that are inconvenient to handle in typical deep learning systems. Moreover, existing implementations only work well for datasets that allow efficient random access (e.g., that can be loaded entirely in memory), as is done in the PyTorch Opacus library. As a workaround, most deep learning systems using DP generate fixed-size batches by globally shuffling the examples in the dataset, but reporting privacy parameters that assume Poisson subsampling was used.
We scalably implement Poisson subsampling by using the Map-Reduce framework to generate batches. We use Apache beam in Python, which can be implemented on distributed platforms, such as Apache Flink, Apache Spark, and Google Cloud Dataflow. In order to generate fixed-size batches required for the downstream training, we also modify the privacy analysis to handle truncated batches and pad the batches to a fixed size. This is visualized in the following figure.
Visualization of the Map-Reduce–based implementation of Poisson subsampling. The first “Map” operation samples, for each example, a set of indices of batches to which it belongs (each index is included independently with some probability). The “Reduce” operation groups all examples that fall in the same batch. The final “Map” operation truncates batches that exceed a pre-specified maximum size, or pads dummy elements (with weight=0) to batches that are under the maximum.
Experimental evaluation
We run DP-SGD training in JAX using the Criteo Display Ads pCTR Dataset, which contains around 46 million examples from a week of Criteo ads traffic. Each example has 13 integer features and 26 categorical features, and the objective is to predict the probability of clicking on an ad given these features. We evaluate DP-SGD using the following batch sampling algorithms: (i) deterministic batches, which partition the data into batches in the order it is given; (ii) Poisson subsampled batches; and (iii) shuffled batches with our lower bound on privacy analysis.
The noise scales σ for these different batch sampling algorithms are plotted below for a range of privacy parameters. On the top plot, we fix the privacy parameters at ε = 5 and δ = 2.7 × 10-8 ( typical values used in applications, where δ is of the order of the reciprocal of the number of training examples) and vary the (expected) batch size from 210 (1024) to 218 (262144). On the bottom plot, we fix the batch size at 216 (65536) for concreteness with δ = 2.7 × 10-8 and vary ε from 1 to 256. The number of epochs is fixed at five for both plots, where an epoch refers to one pass of training over the entire dataset. Our lower bound (orange line) shows that the noise scale required for DP-SGD with shuffling is significantly larger than the noise scale required when using Poisson subsampling, except at high ε where Poisson subsampling has higher σ. In other words, DP-SGD with shuffling requires more noise to be injected during training as compared to when using Poisson subsampling at the same privacy level.
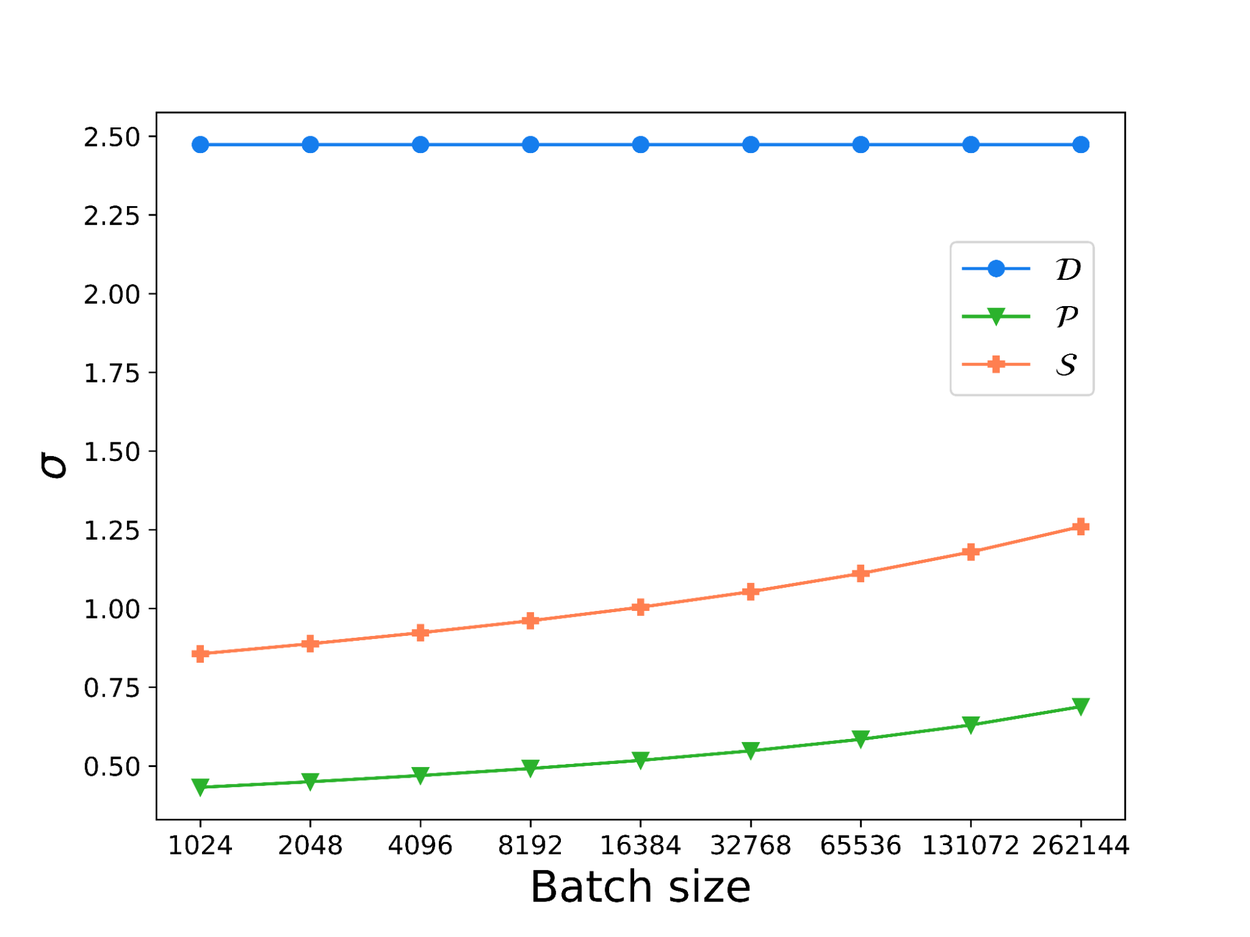
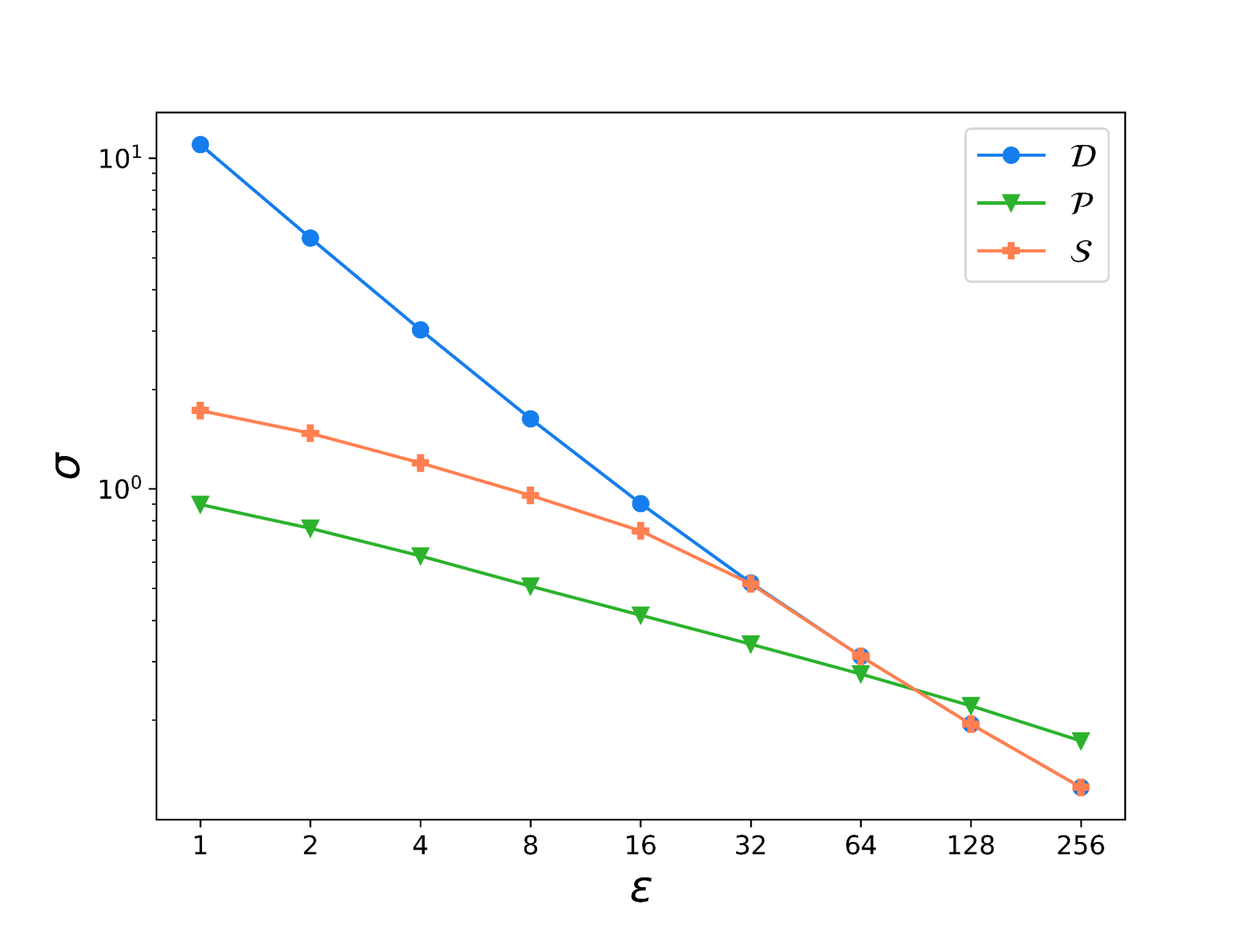
Plots showing how noise scale σ varies with the batch size (top) and with ε (bottom).
As expected, the higher noise injected during training translates to trained models with worse performance. Namely, we find that for the same setting of parameters, the model performance, as measured in terms of area under the curve (AUC) is worse for larger noise scales. We observe that DP-SGD with shuffling (with our lower bound analysis) performs worse than with Poisson subsampling in the high privacy (small ε) regime. An implementation of DP-SGD with shuffling that uses the correct privacy accounting would have to add at least this much noise, and hence this suggests that with the correct corresponding privacy analysis, DP-SGD with shuffling would only perform worse.
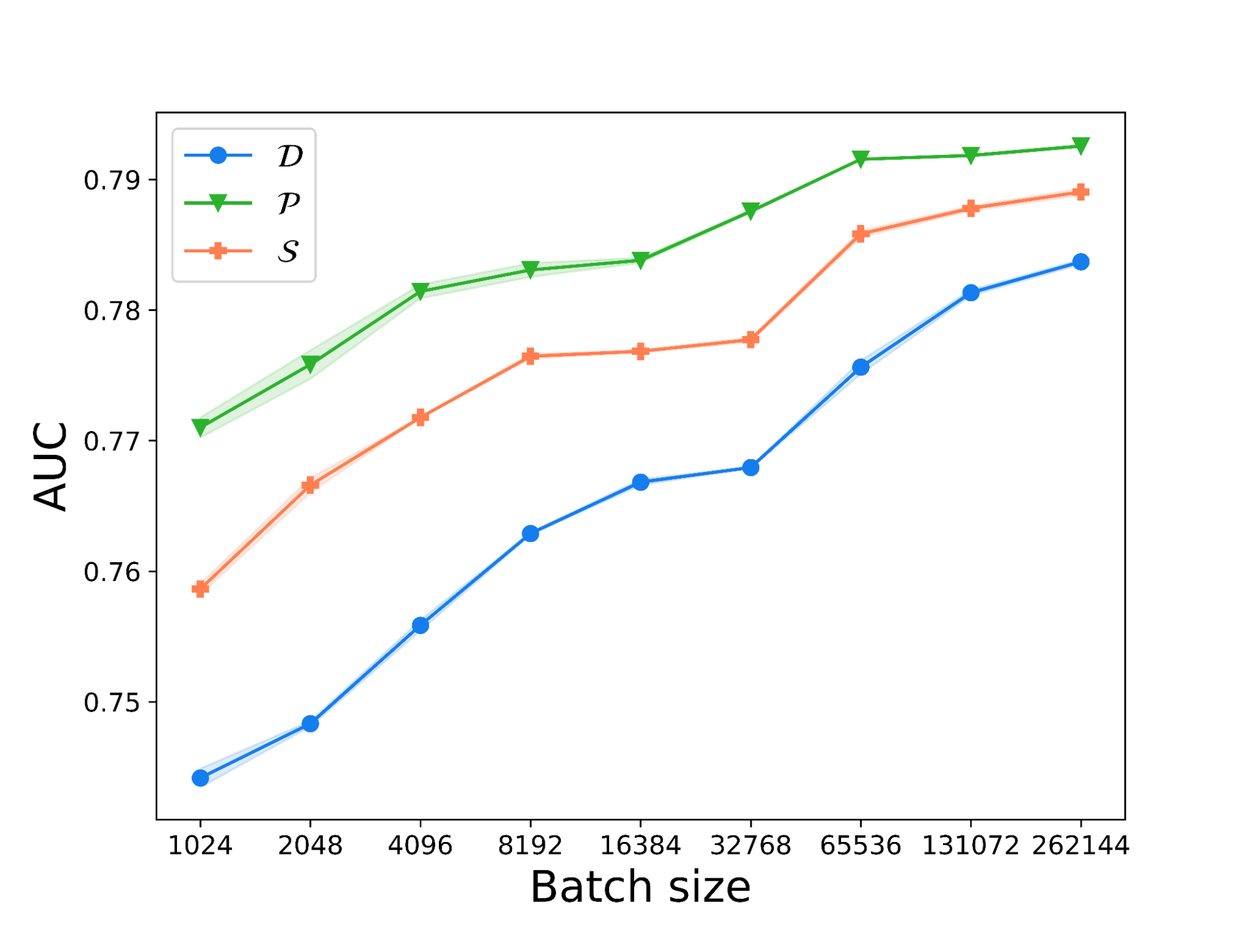
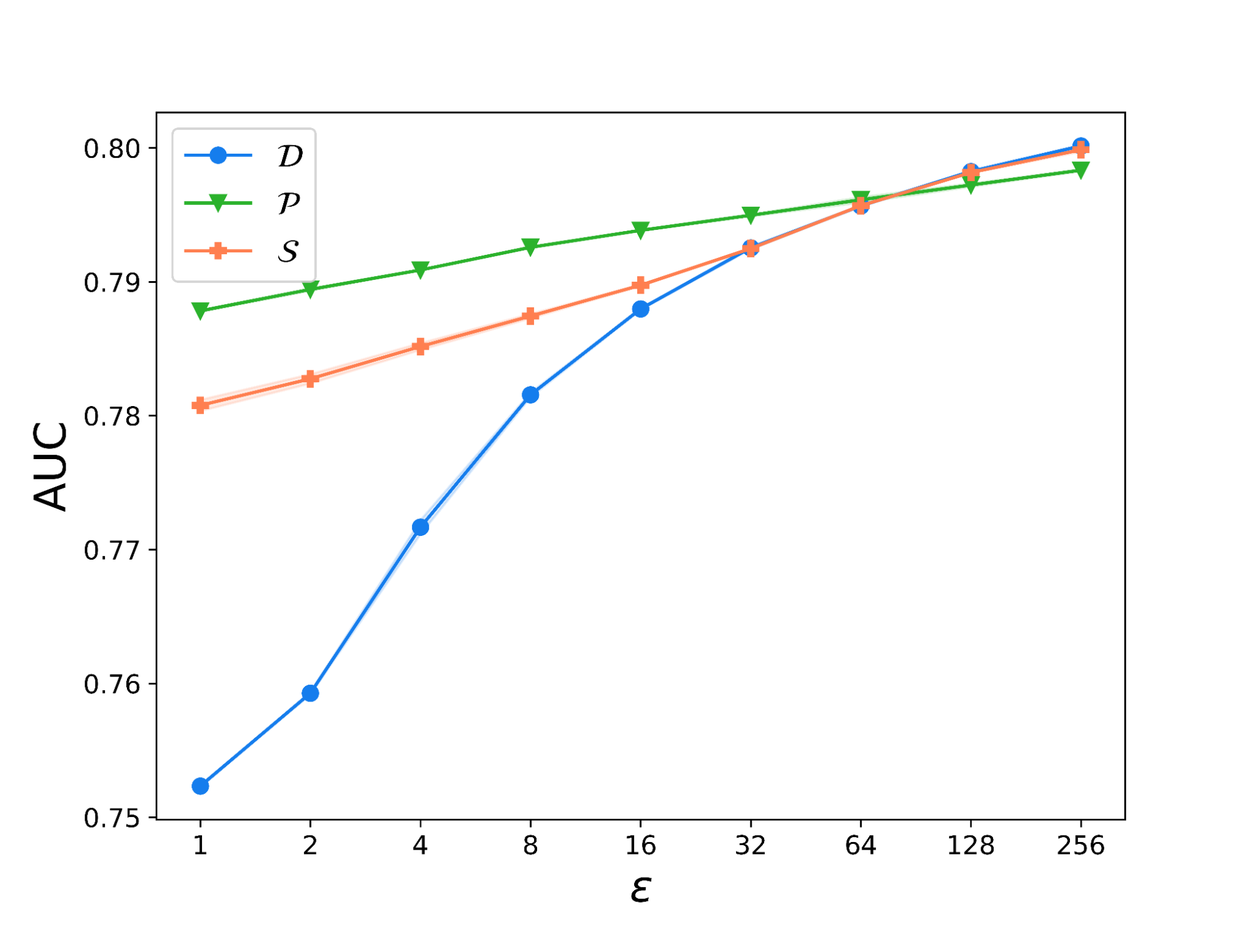
Plots showing how the model performance (as measured by AUC) varies with the batch size (top) and with ε (bottom).
Conclusion
Our work identifies a critical gap in the privacy analysis of DP-SGD implementations. We show that the common practice of shuffling training data into fixed-size mini-batches can lead to weaker privacy protection than previously assumed. This vulnerability stems from a mismatch between the practical implementation and the theoretical analysis, which often relies on the assumption of Poisson subsampling for construction of mini-batches.
To address this issue, we propose a scalable implementation of Poisson subsampling using the Map-Reduce framework. Our experimental evaluation on an ad-click prediction dataset demonstrates that this approach provides better model performance for the same privacy guarantee, compared to traditional technique of shuffling, particularly in high-privacy regimes with smaller ε values. These findings highlight the importance of rigorous analysis and implementation of privacy-preserving ML algorithms to ensure robust protection of user data.
Acknowledgements
This work was carried out in collaboration with Badih Ghazi, Ravi Kumar, Pasin Manurangsi, Amer Sinha and Chiyuan Zhang.







