Quantum Supremacy Using a Programmable Superconducting Processor
October 23, 2019
Posted by John Martinis, Chief Scientist Quantum Hardware and Sergio Boixo, Chief Scientist Quantum Computing Theory, Google AI Quantum
Physicists have been talking about the power of quantum computing for over 30 years, but the questions have always been: will it ever do something useful and is it worth investing in? For such large-scale endeavors it is good engineering practice to formulate decisive short-term goals that demonstrate whether the designs are going in the right direction. So, we devised an experiment as an important milestone to help answer these questions. This experiment, referred to as a quantum supremacy experiment, provided direction for our team to overcome the many technical challenges inherent in quantum systems engineering to make a computer that is both programmable and powerful. To test the total system performance we selected a sensitive computational benchmark that fails if just a single component of the computer is not good enough.
Today we published the results of this quantum supremacy experiment in the Nature article, “Quantum Supremacy Using a Programmable Superconducting Processor”. We developed a new 54-qubit processor, named “Sycamore”, that is comprised of fast, high-fidelity quantum logic gates, in order to perform the benchmark testing. Our machine performed the target computation in 200 seconds, and from measurements in our experiment we determined that it would take the world’s fastest supercomputer 10,000 years to produce a similar output.
 |
| Left: Artist's rendition of the Sycamore processor mounted in the cryostat. (Full Res Version; Forest Stearns, Google AI Quantum Artist in Residence) Right: Photograph of the Sycamore processor. (Full Res Version; Erik Lucero, Research Scientist and Lead Production Quantum Hardware) |
To get a sense of how this benchmark works, imagine enthusiastic quantum computing neophytes visiting our lab in order to run a quantum algorithm on our new processor. They can compose algorithms from a small dictionary of elementary gate operations. Since each gate has a probability of error, our guests would want to limit themselves to a modest sequence with about a thousand total gates. Assuming these programmers have no prior experience, they might create what essentially looks like a random sequence of gates, which one could think of as the “hello world” program for a quantum computer. Because there is no structure in random circuits that classical algorithms can exploit, emulating such quantum circuits typically takes an enormous amount of classical supercomputer effort.
Each run of a random quantum circuit on a quantum computer produces a bitstring, for example 0000101. Owing to quantum interference, some bitstrings are much more likely to occur than others when we repeat the experiment many times. However, finding the most likely bitstrings for a random quantum circuit on a classical computer becomes exponentially more difficult as the number of qubits (width) and number of gate cycles (depth) grow.
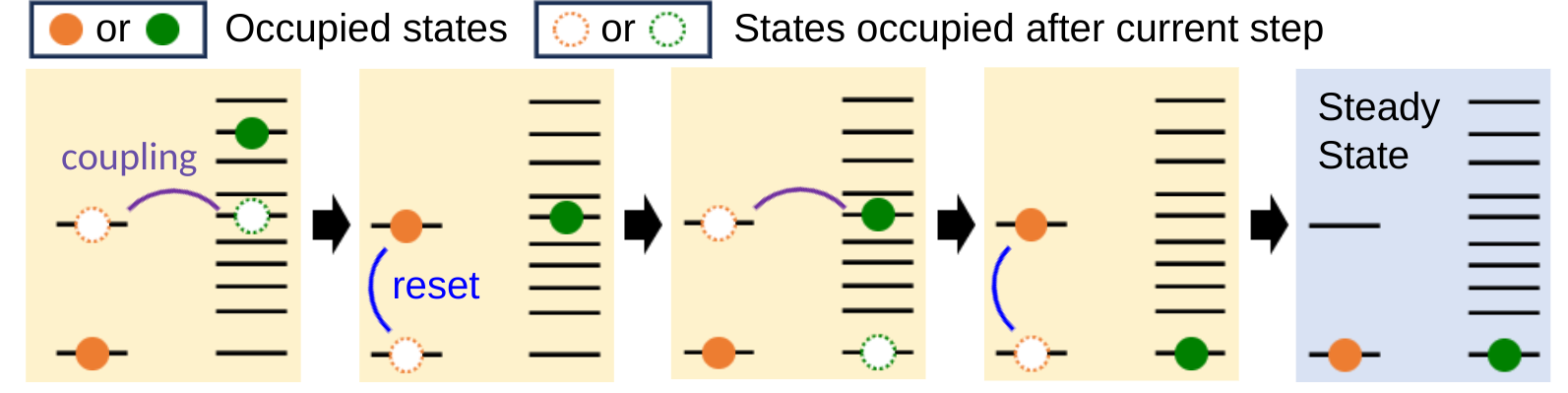
 |
| Process for demonstrating quantum supremacy. |
 |
| Estimate of the equivalent classical computation time assuming 1M CPU cores for quantum supremacy circuits as a function of the number of qubits and number of cycles for the Schrödinger-Feynman algorithm. The star shows the estimated computation time for the largest experimental circuits. |
The Sycamore Processor
The quantum supremacy experiment was run on a fully programmable 54-qubit processor named “Sycamore.” It’s comprised of a two-dimensional grid where each qubit is connected to four other qubits. As a consequence, the chip has enough connectivity that the qubit states quickly interact throughout the entire processor, making the overall state impossible to emulate efficiently with a classical computer.
The success of the quantum supremacy experiment was due to our improved two-qubit gates with enhanced parallelism that reliably achieve record performance, even when operating many gates simultaneously. We achieved this performance using a new type of control knob that is able to turn off interactions between neighboring qubits. This greatly reduces the errors in such a multi-connected qubit system. We made further performance gains by optimizing the chip design to lower crosstalk, and by developing new control calibrations that avoid qubit defects.
We designed the circuit in a two-dimensional square grid, with each qubit connected to four other qubits. This architecture is also forward compatible for the implementation of quantum error-correction. We see our 54-qubit Sycamore processor as the first in a series of ever more powerful quantum processors.
 |
| Heat map showing single- (e1; crosses) and two-qubit (e2; bars) Pauli errors for all qubits operating simultaneously. The layout shown follows the distribution of the qubits on the processor. (Courtesy of Nature magazine.) |
Testing Quantum Physics
To ensure the future utility of quantum computers, we also needed to verify that there are no fundamental roadblocks coming from quantum mechanics. Physics has a long history of testing the limits of theory through experiments, since new phenomena often emerge when one starts to explore new regimes characterized by very different physical parameters. Prior experiments showed that quantum mechanics works as expected up to a state-space dimension of about 1000. Here, we expanded this test to a size of 10 quadrillion and find that everything still works as expected. We also tested fundamental quantum theory by measuring the errors of two-qubit gates and finding that this accurately predicts the benchmarking results of the full quantum supremacy circuits. This shows that there is no unexpected physics that might degrade the performance of our quantum computer. Our experiment therefore provides evidence that more complex quantum computers should work according to theory, and makes us feel confident in continuing our efforts to scale up.
Applications
The Sycamore quantum computer is fully programmable and can run general-purpose quantum algorithms. Since achieving quantum supremacy results last spring, our team has already been working on near-term applications, including quantum physics simulation and quantum chemistry, as well as new applications in generative machine learning, among other areas.
We also now have the first widely useful quantum algorithm for computer science applications: certifiable quantum randomness. Randomness is an important resource in computer science, and quantum randomness is the gold standard, especially if the numbers can be self-checked (certified) to come from a quantum computer. Testing of this algorithm is ongoing, and in the coming months we plan to implement it in a prototype that can provide certifiable random numbers.
What’s Next?
Our team has two main objectives going forward, both towards finding valuable applications in quantum computing. First, in the future we will make our supremacy-class processors available to collaborators and academic researchers, as well as companies that are interested in developing algorithms and searching for applications for today’s NISQ processors. Creative researchers are the most important resource for innovation — now that we have a new computational resource, we hope more researchers will enter the field motivated by trying to invent something useful.
Second, we’re investing in our team and technology to build a fault-tolerant quantum computer as quickly as possible. Such a device promises a number of valuable applications. For example, we can envision quantum computing helping to design new materials — lightweight batteries for cars and airplanes, new catalysts that can produce fertilizer more efficiently (a process that today produces over 2% of the world’s carbon emissions), and more effective medicines. Achieving the necessary computational capabilities will still require years of hard engineering and scientific work. But we see a path clearly now, and we’re eager to move ahead.
Acknowledgements
We’d like to thank our collaborators and contributors — University of California Santa Barbara, NASA Ames Research Center, Oak Ridge National Laboratory, Forschungszentrum Jülich, and many others who helped along the way.
-
Labels:
- Quantum