Evolving Reinforcement Learning Algorithms
April 22, 2021
Posted by John D. Co-Reyes, Research Intern and Yingjie Miao, Senior Software Engineer, Google Research
A long-term, overarching goal of research into reinforcement learning (RL) is to design a single general purpose learning algorithm that can solve a wide array of problems. However, because the RL algorithm taxonomy is quite large, and designing new RL algorithms requires extensive tuning and validation, this goal is a daunting one. A possible solution would be to devise a meta-learning method that could design new RL algorithms that generalize to a wide variety of tasks automatically.
In recent years, AutoML has shown great success in automating the design of machine learning components, such as neural networks architectures and model update rules. One example is Neural Architecture Search (NAS), which has been used to develop better neural network architectures for image classification and efficient architectures for running on phones and hardware accelerators. In addition to NAS, AutoML-Zero shows that it’s even possible to learn the entire algorithm from scratch using basic mathematical operations. One common theme in these approaches is that the neural network architecture or the entire algorithm is represented by a graph, and a separate algorithm is used to optimize the graph for certain objectives.
These earlier approaches were designed for supervised learning, in which the overall algorithm is more straightforward. But in RL, there are more components of the algorithm that could be potential targets for design automation (e.g., neural network architectures for agent networks, strategies for sampling from the replay buffer, overall formulation of the loss function), and it is not always clear what the best model update procedure would be to integrate these components. Prior efforts for the automation RL algorithm discovery have focused primarily on model update rules. These approaches learn the optimizer or RL update procedure itself and commonly represent the update rule with a neural network such as an RNN or CNN, which can be efficiently optimized with gradient-based methods. However, these learned rules are not interpretable or generalizable, because the learned weights are opaque and domain specific.
In our paper “Evolving Reinforcement Learning Algorithms”, accepted at ICLR 2021, we show that it’s possible to learn new, analytically interpretable and generalizable RL algorithms by using a graph representation and applying optimization techniques from the AutoML community. In particular, we represent the loss function, which is used to optimize an agent’s parameters over its experience, as a computational graph, and use Regularized Evolution to evolve a population of the computational graphs over a set of simple training environments. This results in increasingly better RL algorithms, and the discovered algorithms generalize to more complex environments, even those with visual observations like Atari games.
RL Algorithm as a Computational Graph
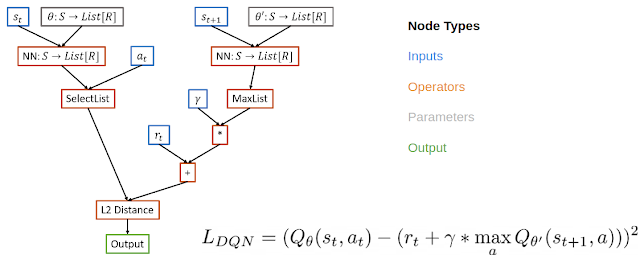
Inspired by ideas from NAS, which searches over the space of graphs representing neural network architectures, we meta-learn RL algorithms by representing the loss function of an RL algorithm as a computational graph. In this case, we use a directed acyclic graph for the loss function, with nodes representing inputs, operators, parameters and outputs. For example, in the computational graph for DQN, input nodes include data from the replay buffer, operator nodes include neural network operators and basic math operators, and the output node represents the loss, which will be minimized with gradient descent.
There are a few benefits of such a representation. This representation is expressive enough to define existing algorithms but also new, undiscovered algorithms. It is also interpretable. This graph representation can be analyzed in the same way as human designed RL algorithms, making it more interpretable than approaches that use black box function approximators for the entire RL update procedure. If researchers can understand why a learned algorithm is better, then they can both modify the internal components of the algorithm to improve it and transfer the beneficial components to other problems. Finally, the representation supports general algorithms that can solve a wide variety of problems.
 |
| Example computation graph for DQN which computes the squared Bellman error. |
We implemented this representation using the PyGlove library, which conveniently turns the graph into a search space that can be optimized with regularized evolution.
Evolving RL Algorithms
We use an evolutionary based approach to optimize the RL algorithms of interest. First, we initialize a population of training agents with randomized graphs. This population of agents is trained in parallel over a set of training environments. The agents first train on a hurdle environment — an easy environment, such as CartPole, intended to quickly weed out poorly performing programs.
If an agent cannot solve the hurdle environment, the training is stopped early with a score of zero. Otherwise the training proceeds to more difficult environments (e.g., Lunar Lander, simple MiniGrid environments, etc.). The algorithm performance is evaluated and used to update the population, where more promising algorithms are further mutated. To reduce the search space, we use a functional equivalence checker which will skip over newly proposed algorithms if they are functionally the same as previously examined algorithms. This loop continues as new mutated candidate algorithms are trained and evaluated. At the end of training, we select the best algorithm and evaluate its performance over a set of unseen test environments.
The population size in the experiments was around 300 agents, and we observed the evolution of good candidate loss functions after 20-50 thousand mutations, requiring about three days of training. We were able to train on CPUs because the training environments were simple, controlling for the computational and energy cost of training. To further control the cost of training, we seeded the initial population with human-designed RL algorithms such as DQN.
Learned Algorithms
We highlight two discovered algorithms that exhibit good generalization performance. The first is DQNReg, which builds on DQN by adding a weighted penalty on the Q-values to the normal squared Bellman error. The second learned loss function, DQNClipped, is more complex, although its dominating term has a simple form — the max of the Q-value and the squared Bellman error (modulo a constant). Both algorithms can be viewed as a way to regularize the Q-values. While DQNReg adds a soft constraint, DQNClipped can be interpreted as a kind of constrained optimization that will minimize the Q-values if they become too large. We show that this learned constraint kicks in during the early stage of training when overestimating the Q-values is a potential issue. Once this constraint is satisfied, the loss will instead minimize the original squared Bellman error.
A closer analysis shows that while baselines like DQN commonly overestimate Q-values, our learned algorithms address this issue in different ways. DQNReg underestimates the Q-values, while DQNClipped has similar behavior to double dqn in that it slowly approaches the ground truth without overestimating it.
It’s worth pointing out that these two algorithms consistently emerge when the evolution is seeded with DQN. Learning from scratch, the method rediscovers the TD algorithm. For completeness, we release a dataset of top 1000 performing algorithms discovered during evolution. Curious readers could further investigate the properties of these learned loss functions.
 |
| Overestimated values are generally a problem in value-based RL. Our method learns algorithms that have found a way to regularize the Q-values and thus reduce overestimation. |
Learned Algorithms Generalization Performance
Normally in RL, generalization refers to a trained policy generalizing across tasks. However, in this work we’re interested in algorithmic generalization performance, which means how well an algorithm works over a set of environments. On a set of classical control environments, the learned algorithms can match baselines on the dense reward tasks (CartPole, Acrobot, LunarLander) and outperform DQN on the sparser reward task, MountainCar.
 |
| Performance of learned algorithms versus baselines on classical control environments. |
On a set of sparse reward MiniGrid environments, which test a variety of different tasks, we see that DQNReg greatly outperforms baselines on both the training and test environments, in terms of sample efficiency and final performance. In fact, the effect is even more pronounced on the test environments, which vary in size, configuration, and existence of new obstacles, such as lava.
 |
| Training environment performance versus training steps as measured by episode return over 10 training seeds. DQNReg can match or outperform baselines in sample efficiency and final performance. |
 |
| DQNReg can greatly outperform baselines on unseen test environments. |
We visualize the performance of normal DDQN vs. the learned algorithm DQNReg on a few MiniGrid environments. The starting location, wall configuration, and object configuration of these environments are randomized at each reset, which requires the agent to generalize instead of simply memorizing the environment. While DDQN often struggles to learn any meaningful behavior, DQNReg can learn the optimal behavior efficiently.
| DDQN |  |  |  |
| DQNReg (Learned) |  |  |  |
Even on image-based Atari environments we observe improved performance, even though training was on non-image-based environments. This suggests that meta-training on a set of cheap but diverse training environments with a generalizable algorithm representation could enable radical algorithmic generalization.
 |
| Env | DQN | DDQN | PPO | DQNReg |
| Asteroid | 1364.5 | 734.7 | 2097.5 | 2390.4 |
| Bowling | 50.4 | 68.1 | 40.1 | 80.5 |
| Boxing | 88.0 | 91.6 | 94.6 | 100.0 |
| RoadRunner | 39544.0 | 44127.0 | 35466.0 | 65516.0 |
| Performance of learned algorithm, DQNReg, against baselines on several Atari games. Performance is evaluated over 200 test episodes every 1 million steps. |
Conclusion
In this post, we’ve discussed learning new interpretable RL algorithms by representing their loss functions as computational graphs and evolving a population of agents over this representation. The computational graph formulation allows researchers to both build upon human-designed algorithms and study the learned algorithms using the same mathematical toolset as the existing algorithms. We analyzed a few of the learned algorithms and can interpret them as a form of entropy regularization to prevent value overestimation. These learned algorithms can outperform baselines and generalize to unseen environments. The top performing algorithms are available for further analytical study.
We hope that future work will extend to more varied RL settings such as actor critic algorithms or offline RL. Furthermore we hope that this work can lead to machine assisted algorithm development where computational meta-learning can help researchers find new directions to pursue and incorporate learned algorithms into their own work.
Acknowledgements
We thank our co-authors Daiyi Peng, Esteban Real, Sergey Levine, Quoc V. Le, Honglak Lee, and Aleksandra Faust. We also thank Luke Metz for helpful early discussions and feedback on the paper, Hanjun Dai for early discussions on related research ideas, Xingyou Song, Krzysztof Choromanski, and Kevin Wu for helping with infrastructure, and Jongwook Choi for helping with environment selection. Finally we thank Tom Small for designing animations for this post.