Scalable self-improvement for compiler optimization
October 23, 2024
Teodor V. Marinov and Alekh Agarwal, Research Scientists, Google Research
We introduce Iterative BC-Max, a novel technique that aims to reduce the size of the compiled binary files by improving inlining decisions. We describe several benefits to using this approach compared to using off-the-shelf RL algorithms.
Quick links
Most systems we regularly interact with, such as computer operating systems, are faced with the challenge of providing good performance, while managing limited resources like computational time and memory. Since it is challenging to optimally manage these resources, there is increasing interest in the use of machine learning (ML) to make this decision-making data driven rather than heuristic. In compiler optimization, inlining is the process of replacing a call to a function in a program with the body of that function. Inlining for size aims to minimize the size of the final binary file by removing redundant code.
Size is a constraining factor for many applications, such as on-device products, where an increase can hinder performance or even prevent the updating and use of some products. Inlining decisions are a key component that a compiler can optimize, with changes in this decision resulting in a final software binary of significantly different size. Prior work has successfully applied reinforcement learning (RL) algorithms to train effective inlining policies, which have been deployed in several systems. However, most RL algorithms are sensitive to reward signals and require careful hyperparameter tuning to avoid instability and poor performance. Consequently, as the underlying system changes, the RL algorithms must be run again, which is both costly and unreliable in deployment.
To that end, in “Offline Imitation Learning from Multiple Baselines with Applications to Compiler Optimization”, to be presented at the ML For Systems workshop at NeurIPS 2024, we introduce Iterative BC-Max, a novel technique that aims to reduce the size of the compiled binary files by improving inlining decisions. Iterative BC-Max produces a decision-making policy by solving carefully designed supervised learning problems instead of using unstable and computationally demanding RL algorithms. We describe several benefits to using this approach, including fewer compiler interactions, robustness to unreliable reward signals, and only solving binary classification problems instead of more cumbersome RL problems.
Inlining for size
As described in prior work, real code has thousands of functions that call each other, forming a call graph. In the inlining process, a compiler reviews each caller-callee pair to decide if it should be inlined or not. Precisely, at each decision point, we observe a set of features or inputs (called a “state”) associated with the local call graph at the function we are considering for inlining. Each feature captures relevant information for the inlining decision. We have two decisions or actions to choose from {inline, not inline}, and the chosen decision can alter the call graph, influencing future inlining decisions and the final outcome.
Compiler decisions during inlining. “# bbs”, “# users”, “callsite height”, etc. are example features for the inlining decision.
The goal is to design an inlining decision policy, that can make inlining decisions at all observed states as we compile a program, with the goal of reducing the size of the resulting binary.
Algorithmic loop. The compiler asks the inlining policy to make an inlining decision at every function (state in the RL problem). The RL algorithm then updates the inlining policy after receiving the binary size as a reward signal.
Iterative BC-Max: Offline imitation learning for the inlining problem
We address the inlining for size problem by developing Iterative BC-Max, a novel imitation learning approach that constructs and solves a sequence of carefully designed classification problems. When given the input state, the inlining for size classification problem must make an inlining decision by choosing the correct label (i.e., inline or not inline). At a high-level, Iterative BC-Max alternates between program compilation and learning a new compilation policy. The compilation step compiles a large corpus of programs in parallel, while the learning step trains a new policy, performing many updates until the classification problem is solved accurately.
Iterative BC-Max interleaves compilation of all programs with the training of a new policy on classification problems. When applying Iterative BC-Max to the inlining for size problem, we only need to repeat the compilation step a few times, using significantly fewer compilation passes than standard RL algorithms. Further, the binary classification approach is more robust to sparse or unreliable reward signals, which are common for systems problems.
Compiling program corpus
The first step of our algorithm is to compile the program corpus, consisting of representative programs of the binaries we target for size reduction, using a set of baseline policies, so that every program is compiled with every policy. Examples of baseline policies correspond to various hand-designed heuristics or even previously learned policies. This determines the best baseline for each program, that is the baseline whose inlining decisions result in the smallest compiled program size. We note that each program is different, and we want to compile each one in the best possible way.
We create a dataset composed of the best inlining decisions for each state within every program in the corpus to be used in the learning step of the algorithm. Compilation is distributed on as many machines as possible. Further, we introduce additional exploration when compiling a fixed program with an inlining policy by selecting steps in the compilation where we deviate from the inlining policy’s decision. The initial set of baseline policies can be as small as a single policy, which we assume is always available.
Imitation learning for best per-program baseline
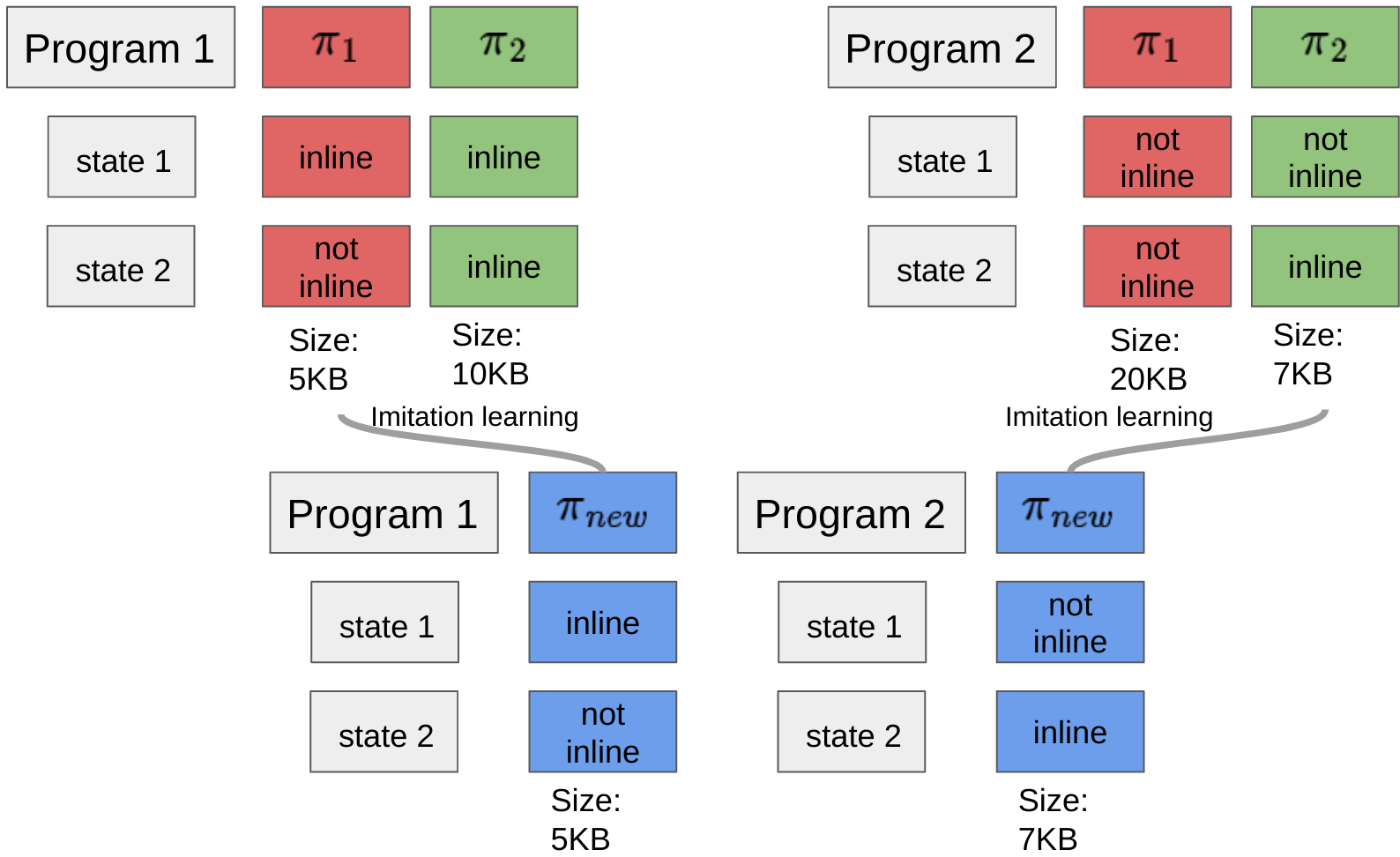
Next, Iterative BC-Max learns a new policy by imitating the sequence of inlining decisions that lead to the best performance for each program as depicted in the figure below. This is achieved by training the policy to match the decision from the inlining dataset, which contains the best sequence of decisions for each program. The dataset saved after compiling the program corpus consists of state-inline decision pairs. The learning algorithm then tries to find a new policy that consists of the inlining decision for every pair in the dataset.
This can be cast as a standard classification problem, where inputs are the observed states and labels are the desired inlining decision for the state, which we collected in the previous step. Such classification problems can be solved using standard ML techniques.
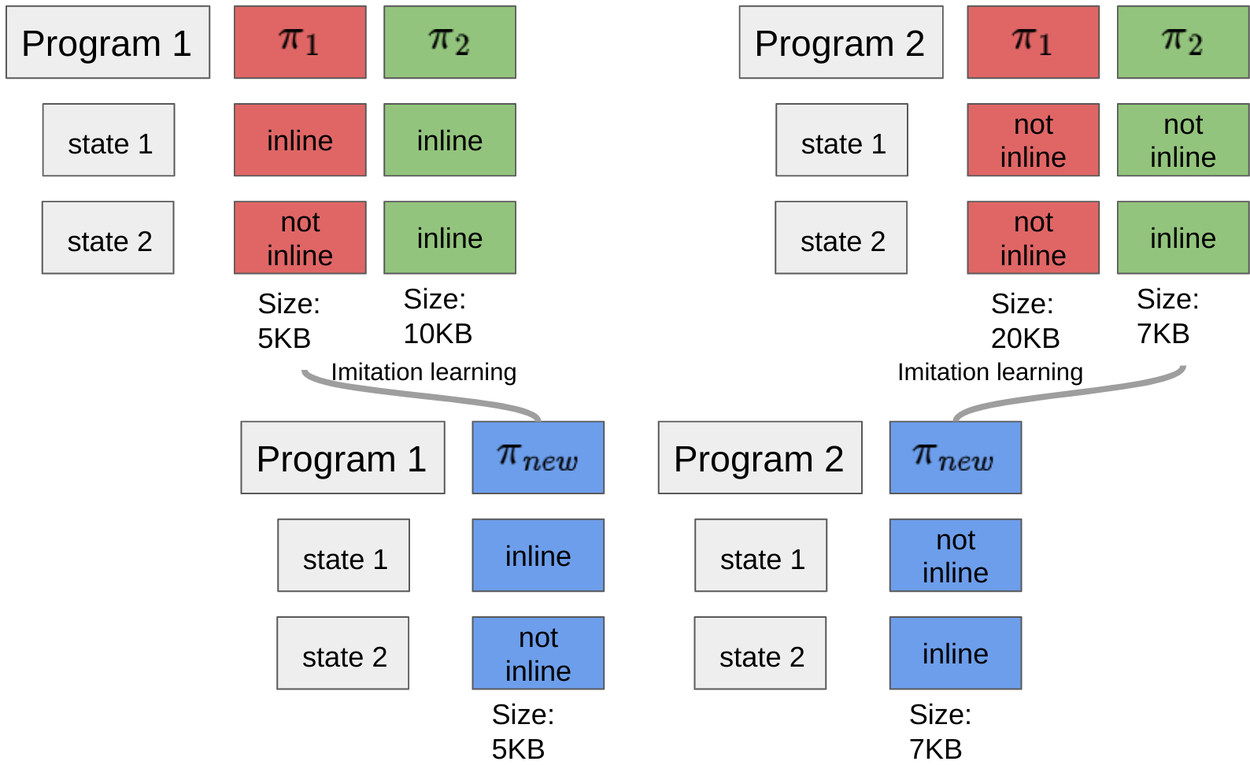
BC-MAX: imitation learning for best per program policy. The best baseline for Program 1 is 𝜋1 , which makes the decision to inline at state 1 and not inline at state 2. The best baseline for Program 2 is 𝜋2 , which makes the decision not to inline at state 1, but to inline at state 2.
Typically, supervised learning algorithms minimize the average classification error, that is the returned policy will be accurate on average across all inlining decisions in the training set. RL experts familiar with imitation learning will recognize that this approach can suffer from distribution shift. That is, the returned policy, trained on the data collected with the baselines, might result in a very different program size, when all inlining decisions are made according to this new policy. To combat such behavior we add weights to the classification objective which leads to a new policy, shown as 𝜋new above, that maximizes the size savings over the worst program in the dataset, making the trained policy more robust to distribution shift.
Complete algorithm
In practice, Iterative BC-Max starts with a set of baseline policies, then at each iteration it alternates between compiling a corpus of programs and learning to follow the best per program inlining decisions. At the end of the K-th iteration the algorithm obtains the new policy, 𝜋new. If the policy has desirable performance in terms of sizes of the compiled programs, we stop and return this policy to be subsequently referenced by the compiler for future inlining decisions. If not, we add 𝜋K+1 to the K previous policies 𝜋1,𝜋2,...,𝜋K. This creates a self-improvement loop where we improve on the best policy so far. In practice the value of K is usually between 5 to 10.
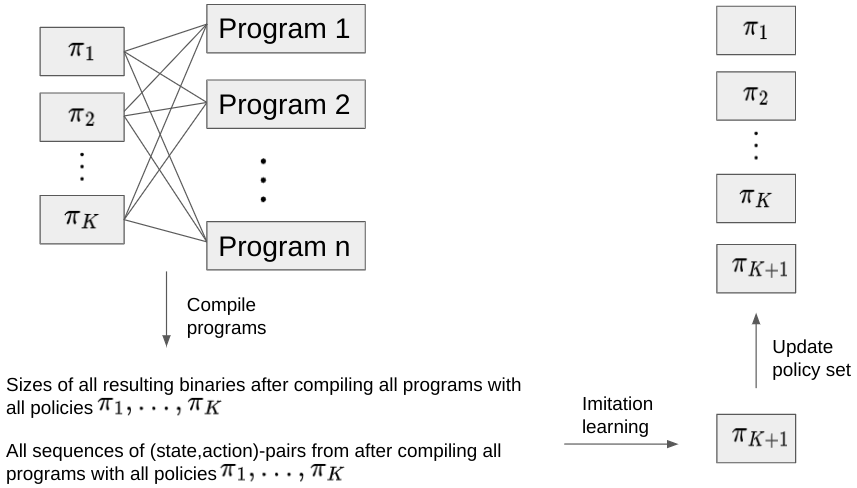
Overview of the Iterative BC-Max algorithm.
Results
We apply Iterative BC-Max to an inlining for size problem where the programs make up a search application binary and there are approximately 30,000 programs. The baseline policy set is initialized with a hand-designed heuristic inlining policy, and another policy trained using an evolutionary strategy. After seven iterations of our algorithm we find a size reduction of approximately 1% compared to the evolutionary strategy baseline. See the paper for more detailed results.
Extensions and future work
Iterative BC-Max is very general and can be applied to multiple different systems optimization problems, even beyond compiler optimization. One immediate application is for register allocation for speed and inlining for speed, where the goal is to produce binaries with improved runtime performance. Other possible applications include optimizing the XLA compiler. We are excited to explore such novel directions.
Acknowledgements
We would like to thank Mircea Trofin for all of his contributions that led to successfully deploying this algorithm, including implementation, help with the compiler side, and fostering tight collaboration with other Google teams. Thanks to Yundi Qian for introducing us to the MLGO effort and initial compiler optimization problems. We also thank Jacob Hegna for help with the RL interface. Finally, thanks to Hans Wennborg and Jin Xin Ng for facilitating the product deployment in external facing Google products.